회귀분석(regression) 이란 무엇일까?
통계에서 가장 유명한 모델을 뽑으라고 한다면, 회귀분석을 뽑습니다. 그만큼 유명하고, 유용합니다. 앞에서 우리가 다루었던 중간, 기말고사 점수 데이터를 예를 들어서 설명해보죠.
mydata <- read.csv("examscore.csv", header = TRUE)
plot(mydata$midterm, mydata$final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 산점도")
중간, 기말고사의 산점도를 살펴보면, 우리는 관찰된 30명의 학생들의 정보를 볼 수 있습니다. 그리고, 이 30명의 중간 기말고사 점수들의 분포를 보면서, 중간고사를 잘 볼수록 기말고사의 점수도 높은 경향을 보인다는 것을 추측할 수 있죠. 즉, 데이터가 우상향하는 형태로 분포되어 있다는 것을 알아 낼 수 있는데, 이러한 경향을 하나의 직선을 사용해서 나타내보면, 다음과 같이 표시할 수 있습니다.
plot(mydata$midterm, mydata$final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 산점도")
abline(5, 1)
위의 코드에서 abline은 직선을 추가시키는 코드인데, 앞의 숫자 5는 교차점, 1은 기울기를 나타냅니다. 이렇게 교차점과 기울기 두개의 값이 정해지면, 우리는 그에 대응하는 직선을 그릴 수 있습니다.
직선을 통한 예측
중간고사의 점수를 x, 기말고사의 점수를 y라고 생각한다면, 교차점 5, 기울기 1인 직선은 다음과 같이 수학적으로 나타낼 수 있습니다.
y=x+5 이 직선이 데이터가 가진 전반적인 흐름을 잘 나타내고 있다고 생각합시다.
만약 우리가 어떤 과목을 수강하고 있는 학생이고, 우리가 가진 데이터가 교수님이 제공한 작년에 이 과목을 수강했던 학생들의 데이터라고 생각해보죠. 그리고 이 과목은 중간고사 점수와 기말고사 점수의 평균을 내서 60점을 A를 주는 과목이라고 가정합시다.
이러한 상황에서, 내가 처음으로 친 중간고사에 50점을 맞은 것을 깨달았습니다. 만약 평균 60점을 넘겨 A를 받기위해서는 70점을 맞아야 할텐데.. 나의 기말고사 점수는 어떻게 될까요? 교수님이 주신 작년 시험 데이터에 들어있는 학생들의 시험점수 정보를 가지고, 미래의 기말고사 점수를 어떻게 예측할 수 있을까요?
기말고사 점수를 예측하는 한가지 방법은 바로 위에서 구한 직선 식에 다음과 같이 x에 50을 입력하여 나온 y의 값을 기말고사 점수의 예측값으로 사용할 수 있을 것 입니다.
ˆy=50+5=55
즉, 우리가 만약 학생 다섯명의 중간고사 점수를 알고 있다면,
c(46, 39, 59, 63, 77) >> [1] 46 39 59 63 77이 학생들의 기말고사 점수의 예측값은 다음과 같게 될 것입니다.
1 * c(46, 39, 59, 63, 77) + 5>> [1] 51 44 64 68 82회귀직선 결정하기
앞에서 제가 그린 직선이 제가 생각하기엔 데이터의 경향을 잘 나타내고 있다고 생각하는데, 어떻게 생각하시나요? 제 친구에게 데이터의 경향을 잘 나타내는 직선을 그리라고 한다면, 같은 직선을 그릴까요? 다음의 직선을 생각해봅시다.
plot(mydata$midterm, mydata$final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 산점도")
abline(5, 1)
abline(-10, 1.5, col = "red")
빨간 직선이 좀 더 그럴싸하지 않을까요? 이렇듯 10명에게 가장 그럴듯한 직선을 그려보라고 한다면, 10명 다 다른 직선을 그릴 것입니다. 모두가 공감할 만한 규칙같은 것이 있다면 좋을텐데 말이죠.
회귀분석에서 사용하는 직선은 하나의 규칙을 통해서 정해지는데, 그것은 다음과 같습니다.
회귀분석 직선을 사용하여 주어진 y 데이터를 x 데이터로 예측했을 경우, 그 차이의 제곱들의 합이 가장 작은 직선을 선택한다.통계학에서 이러한 예측값과 데이터와의 차이를 잔차(residual)이라고 하고, 이러한 잔차들의 제곱합을 Residual sum of square (RSS)라고 부릅니다. 위의 문장을 rss라는 이름의 함수로 만들어 봅시다.
rss <- function(data, line_info){
x <- data[,1]
y <- data[,2]
intercept <- line_info[1]
slope <- line_info[2]
predict_value = intercept + slope * x
result <- sum((y - predict_value)^2)
result
}앞에서 구한 직선(교차점 5, 기울기 1)에 대응하는 rss 함수 값은 다음과 같이 구할 수 있습니다.
rss(mydata[,3:4], c(5, 1))>> [1] 6421빨간색 직선(교차점 −10, 기울기 1.5)은 어떨까요?
rss(mydata[,3:4], c(-10, 1.5))>> [1] 7928.25위에서 살펴본 기준에 따르면 검정색 선이 빨간색 선보다 훨씬 데이터가 분포된 경향을 잘 나타내주는게 됩니다. 그렇다면, 회귀분석 직선은 어떻게 구할 수 있을까요? 즉, 가장 작은 RSS를 만들어내는 (교차점, 기울기)는 어떻게 구할 수 있을까요?
R에는 함수를 정의하고, 그 함수값을 최소값으로 만들어주는 입력값을 찾아주는 함수가 존재합니다. 바로 optim이라는 함수 입니다. 우리가 만들어 놓은 함수 rss의 입력값은 두 개 였죠? 첫번째 입력값은 x와 y 값이 들어있는 데이터였고, 두번째 입력값은 직선에 대한 정보 (교차점, 기울기) 였습니다.
result <- optim(par = c(1, 1), fn = rss, data = mydata[,3:4])
# 찾은 직선 정보확인
result$par>> [1] 13.8833436 0.8967623# 최소로 만든 함수값
result$value>> [1] 5712.789위의 optim 함수는 par 값을 자유자재로 바꿔가면서 rss 값을 체크를 합니다. 그리고, 그 체크 과정을 여러번 반복한 후 가장 작은 함수값을 만들어주는 직선 정보를 우리에게 알려주는데, 그 정보는 result$par에 담겨져 있으며, 그때의 rss 함수값은 result$value안에 저장이 됩니다. 이것을 그래프로 나타내면 다음과 같습니다.
plot(mydata$midterm, mydata$final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "회귀분석 직선 구하기")
abline(5, 1)
abline(-10, 1.5, col = "red")
abline(result$par, col = "blue") # 회귀직선
text(80, 20, paste('회귀식:',
' y =', round(result$par[1], 2), "+", round(result$par[2], 2), "* x"), col = "blue" )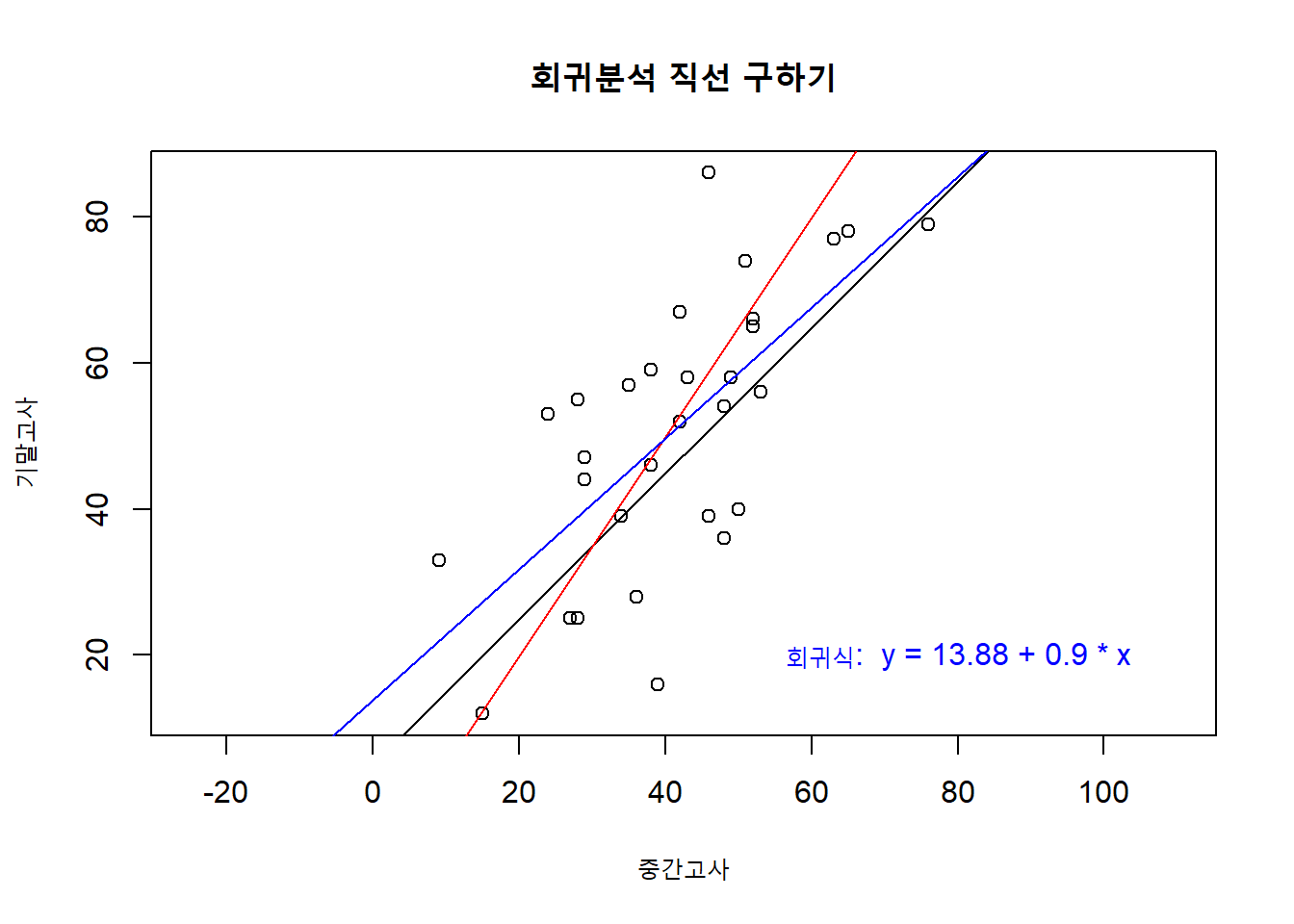
우리가 만약 데이터의 경향을 가장 잘 파악하는 선의 기준을 RSS의 값을 가장 작게 만드는 선이라는 것에 동의를 한다면, 파란색 선이 우리가 찾은 그 모든 선보다 RSS를 가장 작게 만드는 값이므로, 파란색 선이 모든 사람들이 사용해야 하는 선이 됩니다.
회귀분석은 위와 같은 방식으로 구해지며, 이는 R에서도 예외는 아니겠죠.
lm(final ~ midterm, mydata)>>
>> Call:
>> lm(formula = final ~ midterm, data = mydata)
>>
>> Coefficients:
>> (Intercept) midterm
>> 13.8866 0.8967R에서 회귀분석은 lm함수를 이용하여 계산 할 수 있습니다. 위에서 구한 교차점과 기울기를 R에서도 그대로 사용하고 있는 것을 알 수 있습니다. 통계학자들은 회귀분석의 직선식을 위에서 사용한 optim함수를 사용하지 않고도 구할 수 있도록 식을 유도해놓았는데, 바로 다음과 같습니다.
slope=rsysx,intercept=ˉy−slope×ˉx
위의 식에서 r은 이전 시간에 배웠던 상관계수를 나타냅니다. 이 식이 정말로 맞는지, 다음을 통해서 확인해봅시다.
x <- mydata$midterm
y <- mydata$final
# 기울기 b
b <- cor(x, y) * sd(y) / sd(x)
b>> [1] 0.8966817# 교차점 a
a <- mean(y) - b * mean(x)
a>> [1] 13.8866위의 값처럼 잘 작동하네요!
기말고사 점수
RSS를 최소로 만드는 회귀직선으로 우리의 기말고사 점수를 예측해봅시다.
y_hat <- a + b * 50
y_hat>> [1] 58.7206958.7 이라니.. 이제까지 공부했던 방식으로 계속 공부를 한다면 기말고사 점수가 59점 정도밖에 나오지 않는다고 나오네요. A를 받기 위해서는 지금보다 훨씬 더 열심히 공부를 해야겠습니다!
'R > RSTAT101' 카테고리의 다른 글
| [RSTAT101] 8강. 범주형 변수가 포함된 회귀모형 이해하기 (0) | 2023.06.10 |
|---|---|
| [RSTAT101] 7강. R에서 회귀분석 실행하기 (2) | 2023.06.10 |
| [RSTAT101] 5강. 상관계수의 의미와 시각화 (0) | 2023.06.10 |
| [RSTAT101] 4강. 사용자 정의함수와 최빈값 (0) | 2023.06.10 |
| [RSTAT101] 3강. 평균과 중앙값, 분산과 IQR의 관계 이해하기 (1) | 2023.06.10 |




댓글