R에서의 회귀분석
지난 시간에는 회귀분석의 직선이 어떻게 구해지는가에 대하여 알아보았습니다. 오늘은 회귀분석을 R에서 어떻게 하는지에 대하여 알아보도록 합시다. 일단 우리의 데이터를 불러오도록 할게요.
mydata <- read.csv("examscore.csv", header = TRUE)
with(mydata,
plot(midterm, final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 분포")
)
간단한 몸풀기(?) with 구문을 써서 그래프를 그려보았습니다. $을 통해 mydata의 칼럼에 접근하는 것을 with 구문을 사용하여 생략할 수 있습니다. ‘나 이제부터 mydata를 사용할거니까 못찾겠으면 mydata 찾아봐~’ 라고 R에게 알려주는 것이라 생각하면 되겠네요.
지난 시간에 데이터의 경향성을 하나의 직선으로 나타낸 것들 중 RSS (residual sum of square) 값을 가장 작에 만드는 선을 회귀분석 선으로 채택한다는 것을 알아봤습니다. 이 직선을 구하는 이유는 데이터의 변수들끼리의 관계를 알고 있을때, 하나 변수의 정보를 가지고 다른 변수의 값을 예측하는데에 있습니다.
회귀분석 모델
우리 데이터에서는 중간고사 점수(x)를 사용하여 기말고사 점수(y)를 예측하는 것이었죠. 하지만 여기서 문제가 있습니다. 예를 들어, 우리가 가진 데이터에서 두 학생이 중간 고사 점수가 같다고 생각해봅시다. 그리고 기말 고사 점수는 다음과 같다고 생각하죠.
학생 1 - 중간: 57, 기말: 69
학생 2 - 중간: 57, 기말: 64 이 정보를 알고 있을때, 우리가 새로운 학생 3의 중간고사 점수가 57인걸 알고 있다면, 기말고사 점수는 어떻게 예측해야 할까요? 69? 64? 아님 평균을 이용할까요? 뭔가 한 학생의 점수를 사용하기엔 꺼림칙합니다.
이렇게 생각하셨으면 자기 자신을 칭찬해주세요. 방금 당신은 내면에 잠재된 천재성을 발견하셨습니다. 이러한 우리들의 생각을 수식으로 나타내어보면 다음과 같습니다.
\[ Y (\text{final score})= slope \times x (\text{midterm score}) + intercept + noise \]
즉, 우리가 가진 데이터의 기말고사 점수들이 잡음(noise)이 섞여있는 것이라 완전히 믿을 수가 없다는 거죠. 이러한 잡음들이 낀 데이터의 대략적인 트렌드를 구하는 방법이 바로 우리가 지난 시간에 알아본 회귀 직선을 구하는 방법이고, 이 방법을 통해서 구한 직선(기울기, 절편)을 OLS (ordinary least square) 방법을 사용하여 구한 추정값이라고 부릅니다.
R 코드
R에서 회귀분석은 lm 함수를 사용합니다. 함수의 첫번째 입력값은 회귀분석 직선 식이고, 두번째는 데이터입니다.
lm(formula, data, ...)다음과 같이 회귀 분석을 해달라고 R에게 부탁한 후, 결과를 result 변수에 저장합니다. result 변수에 어떤 값들이 들어있는지 보도록 하죠.
result <- lm(final ~ midterm, data = mydata)
attributes(result)>> $names
>> [1] "coefficients" "residuals" "effects" "rank"
>> [5] "fitted.values" "assign" "qr" "df.residual"
>> [9] "xlevels" "call" "terms" "model"
>>
>> $class
>> [1] "lm"위의 결과를 보면, result 변수는 lm이라는 클래스 (지금은 모르셔도 됩니다. lm 함수의 결과를 따로 묶어서 이름을 지어줬다고 생각하면 됩니다.)에 속하며, 가지고 있는 결과값이 12개나 되네요. 제일 첫번째가 당연히 우리가 구하는 회귀분석 직선의 기울기와 절편입니다.
result$coefficients>> (Intercept) midterm
>> 13.8866022 0.8966817이 정보를 가지고 산점도에 쉽게 회귀 직선을 추가할 수 있습니다.
plot(mydata$midterm, mydata$final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 산점도")
abline(result$coefficients) # coefficients에 기울기, 절편 정보가 들어있음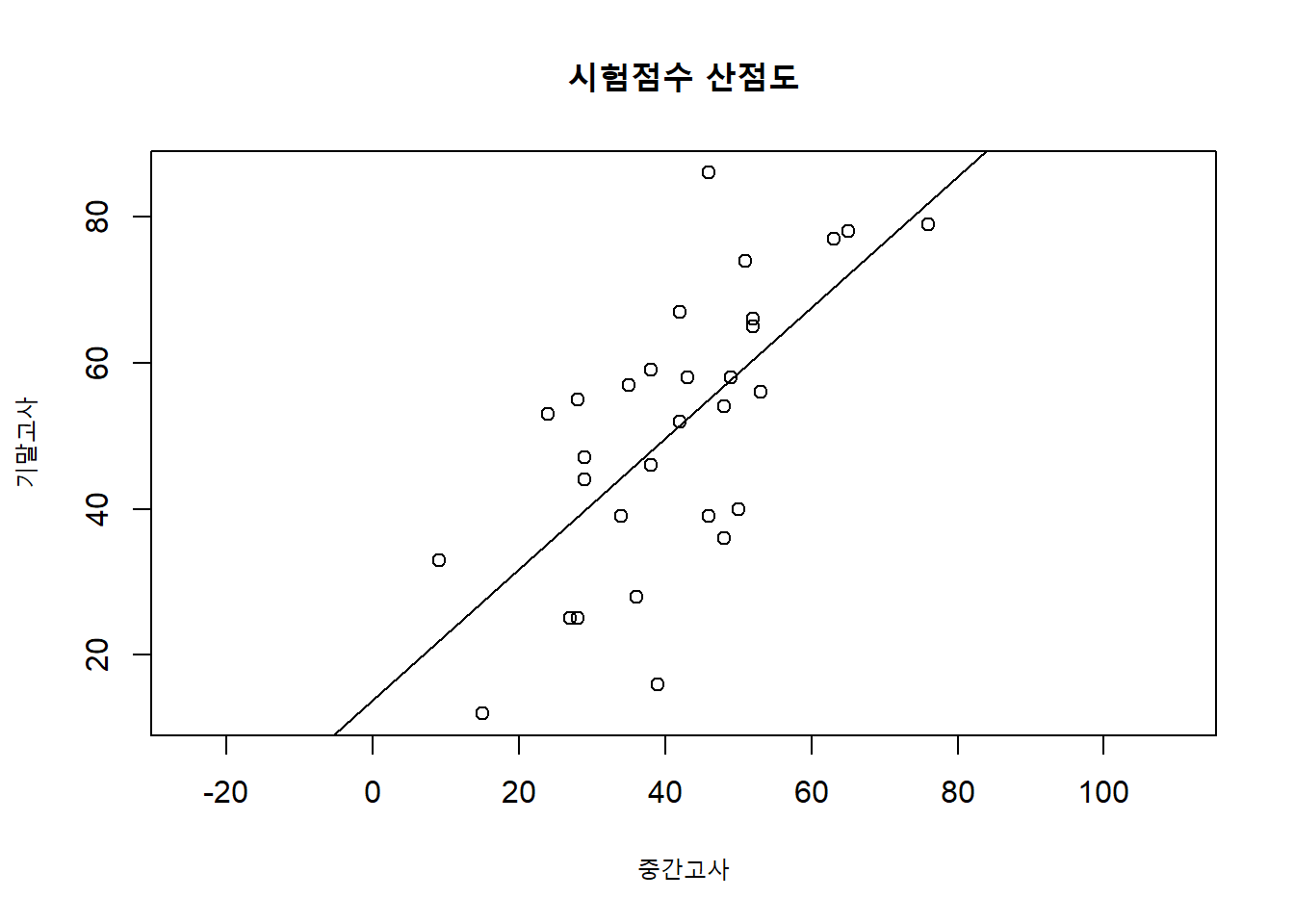
우리가 가진 result 변수의 정보가 어떤 것들이 있는지 정리해서 보여주는 summary함수를 사용해보죠.
summary(result)>>
>> Call:
>> lm(formula = final ~ midterm, data = mydata)
>>
>> Residuals:
>> Min 1Q Median 3Q Max
>> -32.857 -11.175 2.281 10.057 30.866
>>
>> Coefficients:
>> Estimate Std. Error t value Pr(>|t|)
>> (Intercept) 13.8866 8.0195 1.732 0.0943 .
>> midterm 0.8967 0.1842 4.868 3.98e-05 ***
>> ---
>> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>>
>> Residual standard error: 14.28 on 28 degrees of freedom
>> Multiple R-squared: 0.4583, Adjusted R-squared: 0.439
>> F-statistic: 23.69 on 1 and 28 DF, p-value: 3.984e-05앞으로의 통계 공부는 위의 결과를 완전히 이해하는 것에 있다고 해도 과언이 아닐 정도로 한글자 한글자가 무엇을 의미하는지 아셔야 하지만, 그건 아직 나~중에 일이니 겁먹지 마세요! 저 정보를 다 이해 위해서는 상당히 많은 시간 최소 2년 정도는 잡고 공부하셔야 하니, 마음 급하게 먹고 체하시면 안됩니다.
얻을 수 있는 결과값들
우리는 우리가 배운게 무엇이고, 그 배운 내용이 이 결과에서 어떤 곳에 위치하는지 알고 넘어가면 됩니다!
- 입력한 코드 공식
result$call>> lm(formula = final ~ midterm, data = mydata)- 구한 직선 정보
Coefficients 테이블에는 우리가 구한 기울기, 절편값이 들어있는 것을 알 수 있습니다. 오른쪽에 있는 칼럼들은 지금은 넘어가도록 합시다!
result$coefficients>> (Intercept) midterm
>> 13.8866022 0.8966817- 직선을 사용한 예측값, \(\hat{\text{final}}\)
데이터의 중간고사 점수를 직선 방정식에 넣었을 때의 값들에 대한 정보입니다.
head(result$fitted.values) # 처음 6개>> 1 2 3 4 5 6
>> 47.96051 51.54723 61.41073 56.92733 55.13396 59.61737- 잔차 정보.
직선을 구하기 위해서 구했던 에러값들, 잔차 (residuals),에 대한 정보
summary(result$residuals)>> Min. 1st Qu. Median Mean 3rd Qu. Max.
>> -32.857 -11.175 2.281 0.000 10.057 30.866잔차는 다음과 같이 구해집니다.
\[ y_i - \hat{y}_i \quad i=1,...,n \]
다음의 코드가 위의 식을 말해줍니다.
head(mydata$final - result$fitted.values)>> 1 2 3 4 5 6
>> -1.960508 15.452765 -5.410734 -2.927325 -16.133962 14.382630head(result$residuals)>> 1 2 3 4 5 6
>> -1.960508 15.452765 -5.410734 -2.927325 -16.133962 14.382630- 여러 회귀 분석에 관한 그래프
result 변수를 plot 함수에 집어넣으면, R에서 기본적으로 제공하는 네 개의 회귀분석 관련 그래프를 볼 수 있습니다.1 네 개의 그래프 모두 잔차에 관한 그래프인데, 이 그래프를 사용하여 우리가 생각하는 회귀분석 직선을 이용한 예측이 잘 작동하는지를 판단할 수 있기 때문입니다.
par(mfrow = c(2,2))
plot(result)
뭔가 복잡해 보입니다. 하지만 지금 우리가 알아야 할 그래프는 제일 처음 나온 그래프 Residuals vs. Fitted values 입니다. 만약 우리가 기말고사 예측값이 실제 데이터의 기말고사 점수를 모두 정확하게 예측한다면, 에러값(잔차)은 얼마일까요? 0 이겠죠? 이렇게 완벽하게 회귀직선으로 완벽하게 예측할 수 있는 상황은 데이터가 다음과 같이 분포되어 있는 경우 입니다.
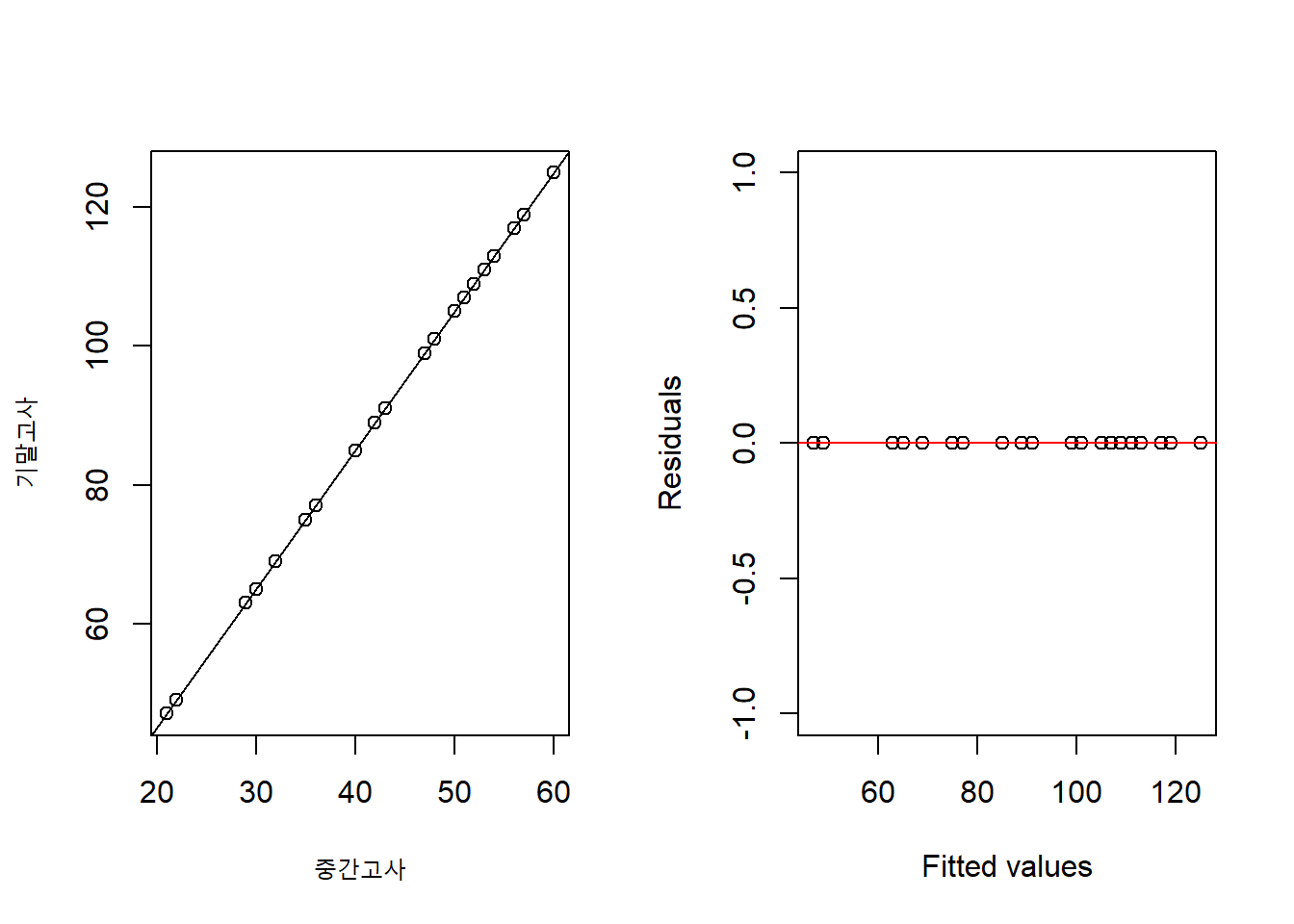
이런 경우는 없겠죠? 왜냐면, 바로 우리가 앞에서 생각했던 기말고사 점수 \(y\)는 잡음 (noise)이 들어있는 것들이기 때문입니다. 그리고 바로 Residuals vs. Fitted values 그래프가 그 잡음들이 각 데이터 포인트 별로 어떻게 분포가 되어 있는지를 보여주는 것입니다.
잔차들이(residuals) 특정한 패턴이 없이 0 근처로 모여있으면 모여있을수록 좋겠죠? 0 근처로 모여있다는 것은 우리의 예측 값들이 회귀분석 직선을 중심으로 위아래로 잘 퍼져있다는 것이며, 특정 예측값들에 영향을 받지 않고 골로구 분포하고 있을 수록 우리가 생각한 회귀분석 식이 잘 작동한다는 것을 나타냅니다.
마치며
이번 시간에 배운 모델처럼 독립 변수(우리의 경우 midterm) 하나를 사용하여 어떤 다른 변수를 예측하는 경우, 우리는 이것을 단순 회귀 (simple regression) 분석을 한다고 말합니다.
꼭 하나만 사용해서 예측을 해야할까요? 만약 주어진 정보가 여러개라면, 그 정보들을 동시에 고려해서 분석해야할 것입니다. 이렇게 고려하는 변수가 여러개가 있는 경우, 우리는 이것을 다중 회귀 (multiple regression) 분석을 한다고 말합니다. 다음 시간에는 다중 회귀에 대하여 알아보겠습니다.
'R > RSTAT101' 카테고리의 다른 글
| [RSTAT101] 9강. 잡음과 정규분포에 대하여 (0) | 2023.06.10 |
|---|---|
| [RSTAT101] 8강. 범주형 변수가 포함된 회귀모형 이해하기 (0) | 2023.06.10 |
| [RSTAT101] 6강. 회귀직선의 의미와 구하는 방법 (0) | 2023.06.10 |
| [RSTAT101] 5강. 상관계수의 의미와 시각화 (0) | 2023.06.10 |
| [RSTAT101] 4강. 사용자 정의함수와 최빈값 (0) | 2023.06.10 |




댓글