범주형(categorical) 변수 시각화
지난 시간에는 R에서 회귀분석을 어떻게 실행하는지 대하여 알아보았습니다. 오늘은 자료가 범주형(categorical) 변수를 포함하고 있을 경우 할 수 있는 회귀분석 대하여 알아봅시다. 일단 우리의 데이터를 불러옵니다.
mydata <- read.csv("examscore.csv", header = TRUE)
with(mydata,
plot(midterm, final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 분포")
)
위의 그래프는 우리의 데이터 중 중간고사, 기말고사 점수를 가지고 나타낸 것이었죠.
head(mydata)>> student_id gender midterm final
>> 1 1 F 38 46
>> 2 2 M 42 67
>> 3 3 F 53 56
>> 4 4 M 48 54
>> 5 5 M 46 39
>> 6 6 M 51 74범례활용과 pch 옵션
데이터 중에 성별을 나타내는 gender 변수가 있는데, 이 정보도 포함해서 시각화를 시켜보도록 합시다.
with(data = mydata,
plot(midterm, final, asp = 1,
pch = c(16, 17)[as.factor(gender)],
col = c("red", "blue")[as.factor(gender)],
main = "성별에 따른 시험성적 분포도",
xlab = "중간고사", ylab = "기말고사")
)
legend(-20, 80,
legend = c("여자", "남자"),
col = c("red", "blue"),
pch = c(16, 17))
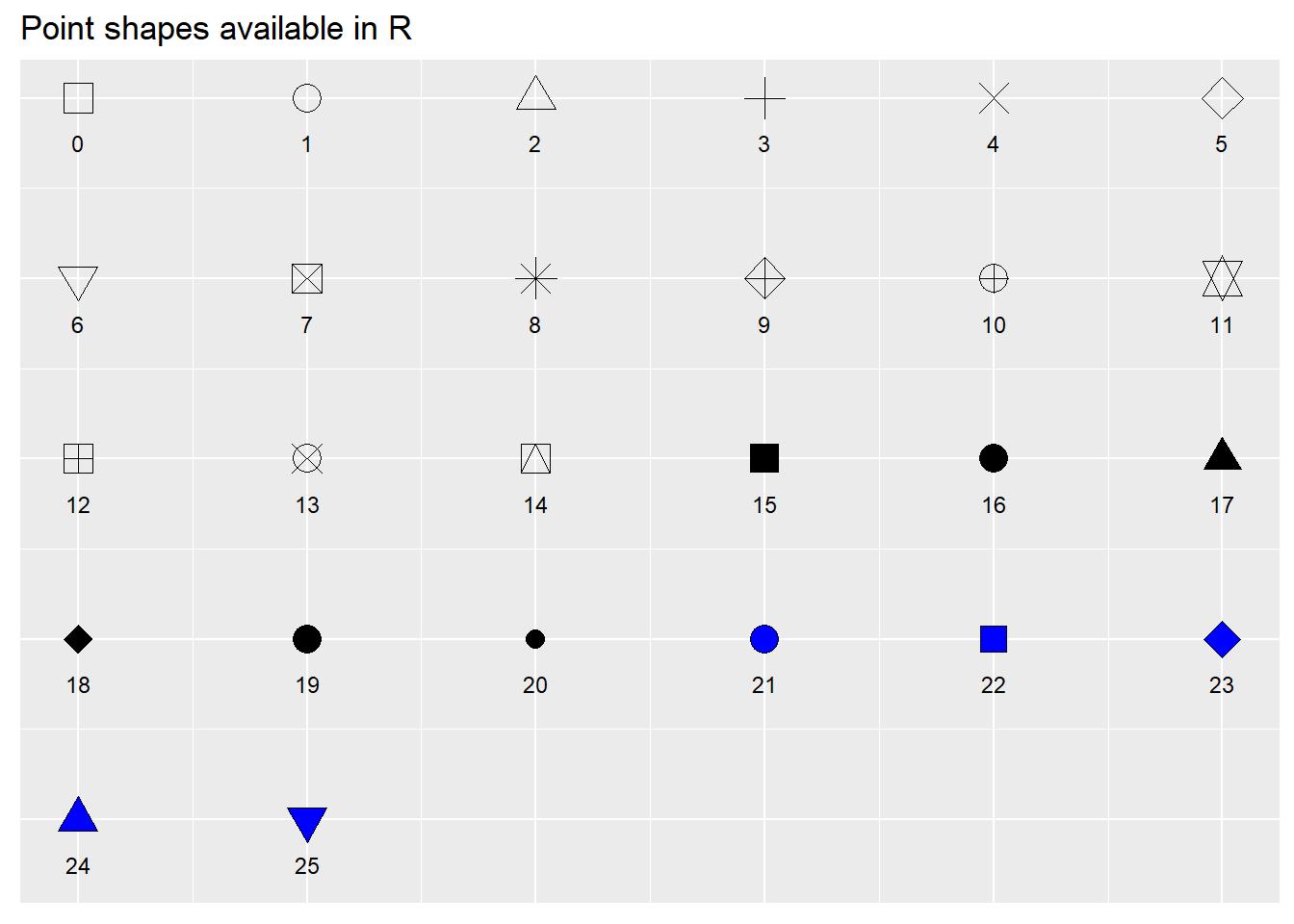
위 그래프에서 점들의 모양을 pch 옵션을 사용하여 지정해줬습니다. 다음의 그림에서와 같이 pch 값에 대응되는 여러가지 모양이 있으니 참고하시면 됩니다. 예를 들어, 그래프에서는 동그라미와 세모를 선택하기 위해서 16과 17을 사용했습니다.
plot함수 아래쪽에 사용된 legend 함수는 그려진 그래프에 범례를 추가하는 함수입니다.
?legend위의 명령어를 콘솔창에서 실행하면 도움말을 불러올 수 있는데, 함수의 첫 두 숫자는 범례가 나타나는 위치를 의미합니다. 위의 그래프에서는 (-20, 80)위치에 범례를 위치 시키기 위하여 -20과 80을 처음 두 값으로 지정하였습니다.
그 다음으로 legend 값으로 우리가 보여줄 항목 이름을 적어주시고, 각 항목에 대응하는 정보들을 col과 pch를 통하여 지정해 줬습니다.
’여자’가 legend 값의 첫 항목이므로, col와 pch의 첫 항목의 값을 각각 ’red’와 동그라미를 나타내는 ’16’으로 설정해줬습니다.
성별에 따른 회귀분석
그래프를 보다보면, 문득 성별이 다르면 회귀직선도 달라야하는 것이 아닌가 하는 생각을 하실 수 있습니다. 뭔가 여자 그룹이 좀 더 위에 위치하고 있는 느낌적인 느낌이죠? 그럴때 어떻게 해야할까요? 우리는 week4-데이터 다루기 시간에 필터링에 대하여 배웠습니다.
data_male <- mydata[mydata$gender == "M",]
data_female <- mydata[mydata$gender == "F",]
head(data_male, 3); head(data_female, 3)>> student_id gender midterm final
>> 2 2 M 42 67
>> 4 4 M 48 54
>> 5 5 M 46 39>> student_id gender midterm final
>> 1 1 F 38 46
>> 3 3 F 53 56
>> 11 11 F 50 40이렇게 나눈 데이터를 가지고 회귀식을 그려보면 어떨까요? 회귀분석을 할 때 사용하는 lm 함수는 다음과 같은 문법을 가지고 있습니다.
lm(종속변수 ~ 독립변수, 사용데이터)즉, lm 함수의 첫 입력값은 모델식을 나타내는 것이고, 두번째 입력값은 회귀분석시 사용되는 데이터를 집어넣어주는 것입니다. 따라서 우리의 회귀분석 코드는 다음과 같이 됩니다.
# regression for each group
model1 <- lm(final~midterm, data_male)
model2 <- lm(final~midterm, data_female)
# coeff.
print("male"); model1$coefficients # male>> [1] "male">> (Intercept) midterm
>> 9.6282664 0.9473853print("female"); model2$coefficients # female >> [1] "female">> (Intercept) midterm
>> 27.8529412 0.6724662결과를 보면 성별에 따른 회귀직선이 다르게 나온다는 것을 알 수 있습니다. 특히, intercept값이 많이 차이가 난다는 것을 알 수 있습니다.
with(data = mydata,
plot(midterm, final, asp = 1,
pch = c(16, 17)[as.factor(gender)],
col = c("red", "blue")[as.factor(gender)],
main = "성별에 따른 시험성적 분포도",
xlab = "중간고사", ylab = "기말고사")
)
legend(-20, 80, legend = c("여자", "남자"),
col = c("red", "blue"), pch = c(16, 17))
abline(model1$coefficients, col = "blue")
abline(model2$coefficients, col = "red")
회귀식의 예측 - predict 함수
자, 그럼 만약 우리가 중간고사를 40점을 맞은 여학생의 기말고사 점수를 예측하고 싶다면 어떻게 해야할까요? 여학생의 기말고사를 예측하고 싶으니, model2를 사용해야 할 것입니다. 새로운 데이터를 가지고 예측하고 싶을땐, predict 함수를 사용하면 됩니다. 단, 데이터를 입력할때 data.frame을 이용해서 변수명을 맞춰줘야합니다. 우리는 model2를 만들때 midterm이라는 변수명을 사용했으므로 다음과 같이 해줍니다.
predict(model2, data.frame(midterm = 40))>> 1
>> 54.75159위의 예측값은 다음과 같이도 얻을 수 있겠죠?
# 레이블 제거
param <- as.numeric(model2$coefficients)
# 직선 식을 이용한 예측
param[1] + 40 * param[2] >> [1] 54.75159만약 우리가 중간고사를 40점을 맞은 남학생의 기말고사 점수를 예측하고 싶다면 어떻게 해야할까요? 이번에는 예측에 사용하는 모델을 남학생 모델로 바꿔주면 될 것 입니다.
predict(model1, data.frame(midterm = 40))>> 1
>> 47.52368다중 회귀분석을 이용한 모델 합치기
그렇다면 한꺼번에 모델을 하나로 쓰는 방법을 없을까요? 일일이 모델을 바꿔주는 것이 아닌 우리가 가진 데이터 포맷을 그대로 사용하면서 성별에 따른 회귀직선을 딱! 알아서 정해줬으면 좋겠는데 말이죠.
다음의 식을 살펴 봅시다.
model3 <- lm(final~midterm + gender, mydata)
model3>>
>> Call:
>> lm(formula = final ~ midterm + gender, data = mydata)
>>
>> Coefficients:
>> (Intercept) midterm genderM
>> 18.9774 0.8808 -6.6563회귀분석 식을 입력하는 첫번째 입력변수에 + 기호를 사용해서 변수를 하나 더 추가해 줬네요! 위의 식을 통계식으로 써본다면, 우리는 다음과 같은 모델을 가정하고 있는 것입니다.
\[ Y = intercept + {coef}_{1} \times x_1 + {coef}_{2} \times x_2 + noise \]
위 식에서 \(Y\)는 기말고사 점수를, \(x_1\)은 중간고사 점수를 \(x_2\)는 성별을 나타내는 변수를 의미할 것입니다. 그런데 분명 성별을 나타내는 변수는 F, M과 같이 문자였는데 어떻게 수식에 넣을까요? 당연히 문자를 수식에 넣을 수 없으니, 숫자로 바꿔주는 과정을 거칩니다. 다음과 같이 말이죠.
c(0, 1)[as.factor(mydata$gender)]>> [1] 0 1 0 1 1 1 1 1 1 1 0 0 1 1 1 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1즉, 우리 데이터에서는 여자의 경우는 0으로, 남자의 경우는 1로 바꿔줘서 데이터를 만드는 것이죠. 그렇다면, 과연 \(coef_2\)가 의미하는 것은 무엇일까요? 위의 결과 값은 다음의 식을 가지고 우리가 기말고사 점수를 예측 할 수 있다는 것을 의미합니다.
\[ \widehat{기말고사} = 18.9774 + 0.8808 \times 중간고사 + (-6.6563) \times 성별 \] 식에서 기말고사 점수의 예측값이라는 의미로 “\(\widehat{기말고사}\)” 기호를 사용했습니다.
중간 고사 40점을 맞은 여학생의 점수를 예측하려면 어떻게 해야할까요? 중간고사 점수는 40이고, 여학생이니까 \(x_2\)의 자리에 0을 넣어주면 됩니다.
\[ \widehat{기말고사} = 18.9774 + 0.8808 \times 40 \] 즉, 다음과 같을 것 입니다.
par <- as.numeric(model3$coefficients)
final_hat <- par[1] + par[2] * 40 + par[3] * 0
final_hat>> [1] 54.20989predict(model3, newdata = data.frame(midterm = 40,
gender = "F"))>> 1
>> 54.20989중간고사 40점을 맞은 남학생의 경우는 어떨까요? 이번엔 성별 변수에 1이 들어가므로 예측식은 다음과 같습니다.
\[ \begin{align} \widehat{기말고사} & = 18.9774 + 0.8808 \times 중간고사 + (-6.6563) \times 1 \\ & = (18.9774 - 6.6563) + 0.8808 \times 중간고사 \\ & = 12.3211 + 0.8808 \times 중간고사 \end{align} \]
오.. 남학생일때는 intercept가 변하는군요!
# 남학생 중간고사 40점
final_hat <- par[1] + par[2] * 40 + par[3] * 1
final_hat>> [1] 47.55363predict(model3, newdata = data.frame(midterm = 40,
gender = "M"))>> 1
>> 47.55363model3 시각화
이것을 이용해서 model3의 회귀직선을 그래프에 표시할 수 있습니다.
with(data = mydata,
plot(midterm, final, asp = 1,
pch = c(16, 17)[as.factor(gender)],
col = c("red", "blue")[as.factor(gender)],
main = "성별에 따른 시험성적 분포도",
xlab = "중간고사", ylab = "기말고사")
)
legend(-20, 80, legend = c("여자", "남자"),
col = c("red", "blue"), pch = c(16, 17))
# model 3 coefficients in 'par' variable
abline(par[1], par[2], col = "red")
abline(par[1] + par[3], par[2], col = "blue")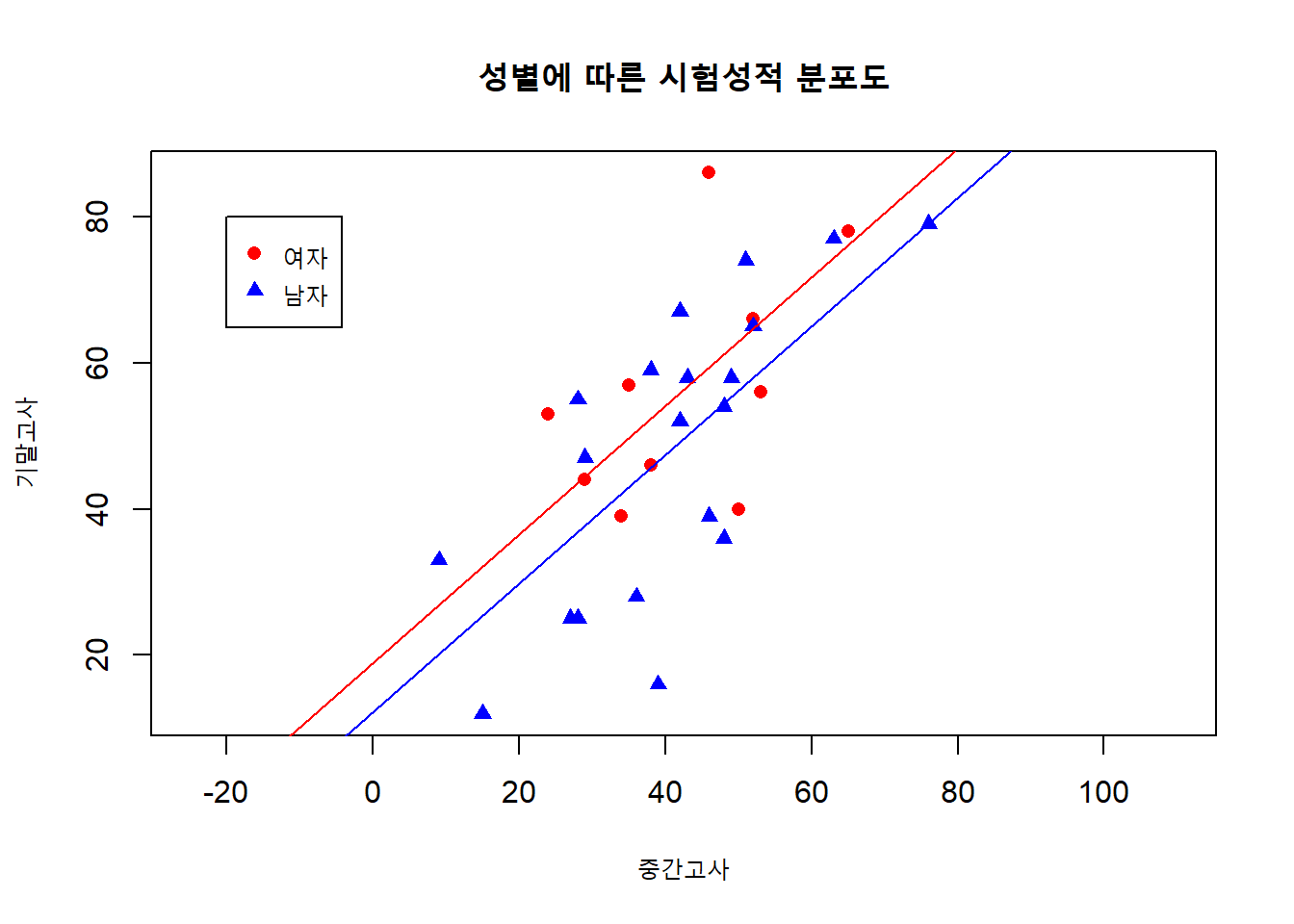
위의 그래프를 보면, 우리가 설정한 model3는 두 그룹이 다른 intercept를 가질 수 있도록 설계가 되어 있는 것을 알 수 있습니다. 뭔가 찝찝하죠? 우리가 생각하기엔 기울기도 그룹마다 다를것 같은데요. 기울기까지 바꿀 수 있는 방법은 없을까요?
교차항을 이용한 회귀분석
두 그룹을 동시에 생각한다는 측면에서 세번째 모델은 우리에게 획기적이었지만, 우리의 기대에는 미치지 못했습니다. 기울기가 달라져야 우리가 생각했던 모델이 나올텐데 말이죠. 다음의 코드를 살펴봅시다.
model4 <- lm(final~midterm + gender + midterm * gender, mydata)
model4>>
>> Call:
>> lm(formula = final ~ midterm + gender + midterm * gender, data = mydata)
>>
>> Coefficients:
>> (Intercept) midterm genderM midterm:genderM
>> 27.8529 0.6725 -18.2247 0.2749아니, 수식에 곱하기를 썼는데 코드가 작동하다니! 회귀분석은 수식에 더하기만 쓰는 줄 알았는데 신기한 일이 벌어졌네요. 어떤 것들이 달라졌는지 알아보기 위하여 앞에서 입력한 모델식을 살펴 봅시다.
\[ \begin{align} Y & = intercept + {coef}_{1} \times x_1 + {coef}_{2} \times x_2 + {coef}_{3} \times (x_1 * x_2) + noise \\ & = intercept + {coef}_{1} \times x_1 + {coef}_{2} \times x_2 + {coef}_{3} \times x_3 + noise \end{align} \]
위의 식에서 우리는 \(x_1\)과 \(x_2\)를 사용해서 (곱해서) \(x_3\)이라는 변수를 하나 더 만들었다고 생각하면 됩니다. 우리가 가진 데이터에 열을 하나 추가 했다고 생각하셔도 됩니다.
c(0, 1)[as.factor(mydata$gender)] * mydata$midterm>> [1] 0 42 0 48 46 51 48 43 28 38 0 0 27 36 29 0 0 0 39 9 76 15 63 28 49
>> [26] 42 0 0 0 52mydata$gen_and_mid <- c(0, 1)[as.factor(mydata$gender)] * mydata$midterm즉, 우리의 데이터가 이러한 칼럼들을 가지고 있다고 생각할 수 있을 것입니다.
head(mydata)>> student_id gender midterm final gen_and_mid
>> 1 1 F 38 46 0
>> 2 2 M 42 67 42
>> 3 3 F 53 56 0
>> 4 4 M 48 54 48
>> 5 5 M 46 39 46
>> 6 6 M 51 74 51이러면 무슨 이점이 있을까요? 중간 고사 40점을 맞은 여학생의 기말고사 점수를 예측 해 보도록 합시다. 예측식에 중간고사(\(x_1\)) 40점, 여학생(\(x_2\))이니까 0을 넣으면 되겠죠?
\[ \begin{align} \widehat{기말고사} & = intercept + {coef}_{1} \times 중간고사 + {coef}_{2} \times 성별 + {coef}_{3} \times (중간고사 * 성별) \\ & = intercept + {coef}_{1} \times 40 + {coef}_{2} \times 0 + {coef}_{3} \times (40 \times 0) \\ & = intercept + {coef}_{1} \times 40 \end{align} \]
앞에서 봤던 회귀 직선 식이 되었습니다. 계수 값을 확인해볼까요?
model4$coefficients[1:2]>> (Intercept) midterm
>> 27.8529412 0.6724662이 숫자들 뭔가 익숙하지 않으신가요..? 여학생만 따로 모아서 회귀직선을 구했던 model2의 계수를 확인해보면, model4에서 여학생의 점수를 예측할 때 model2와 똑같은 직선을 사용한다는 것을 알 수 있습니다.
model2$coefficients>> (Intercept) midterm
>> 27.8529412 0.6724662중간 고사 40점을 맞은 남학생의 경우는 어떨까요? 예측식에 중간고사(\(x_1\)) 40점, 남학생(\(x_2\))이니까 1을 넣으면 되겠죠?
\[ \begin{align} \widehat{기말고사} & = intercept + {coef}_{1} \times 중간고사 + {coef}_{2} \times 성별 + {coef}_{3} \times (중간고사 * 성별) \\ & = intercept + {coef}_{1} \times 40 + {coef}_{2} \times 1 + {coef}_{3} \times (40 \times 1) \\ & = (intercept + {coef}_{2}) + ({coef}_{1} + {coef}_{3}) \times 40 \end{align} \]
남학생의 예측식을 보면,
{{% alert note %}} 회귀식의 coef_2 와 coef_3가 여학생 모델에서 사용했던 절편과 기울기값을 각각 조정해주는 것을 알 수 있습니다. {{% /alert %}}
남학생 모델은 어떤 절편과 기울기값을 갖게 되었을까요?
par <- model4$coefficients
# intercept for male
sum(par[c(1, 3)])>> [1] 9.628266# slope for male
sum(par[c(2, 4)])>> [1] 0.9473853이 결과 역시 앞에서 구했던 남학생만 따로 모아서 회귀분석을 했던 model1의 직선식과 같다는 것을 알 수 있습니다.
model1$coefficients>> (Intercept) midterm
>> 9.6282664 0.9473853즉, 우리가 설정한 model4가 model1과 model2를 동시에 포함하고 있다는 것이죠! 따라서 model4의 회귀직선을 그래프에 나타낸다면 다음과 같이 두 개의 직선이 될 것입니다.
with(data = mydata,
plot(midterm, final, asp = 1,
pch = c(16, 17)[as.factor(gender)],
col = c("red", "blue")[as.factor(gender)],
main = "성별에 따른 시험성적 분포도",
xlab = "중간고사", ylab = "기말고사")
)
legend(-20, 80, legend = c("여자", "남자"),
col = c("red", "blue"), pch = c(16, 17))
par <- model4$coefficients
abline(c(sum(par[c(1, 3)]), sum(par[c(2, 4)])), col = "blue")
abline(c(par[1], par[2]), col = "red")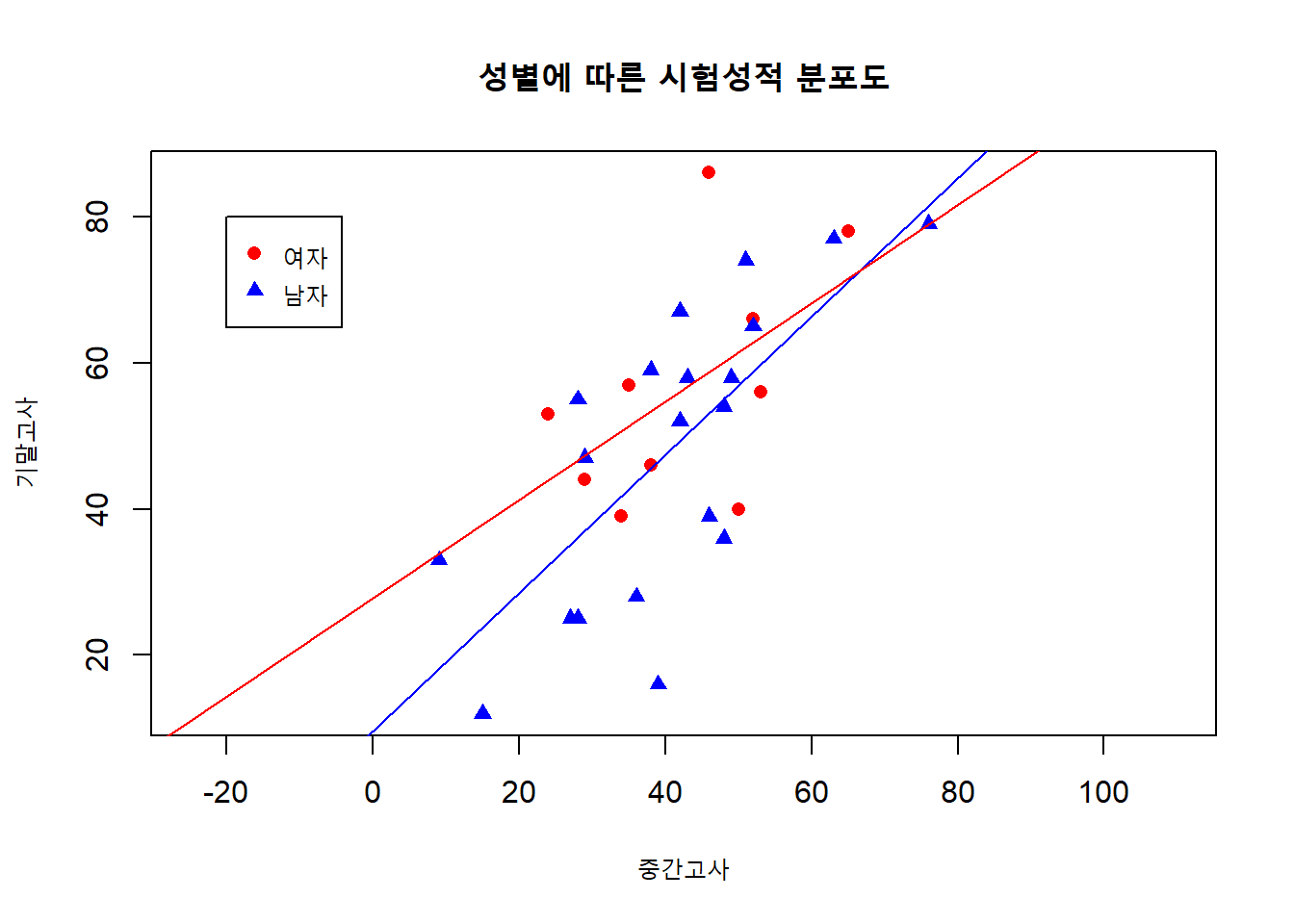
마치며
우리가 이제까지 회귀분석을 이야기 하면서 이야기 하지 않은 항이 하나 있습니다. 바로 잡음(noise)항 입니다. 우리가 모델을 구성할 때 사용한 잡음은 어떠한 특성을 갖고 있어야 좋을까요? 다음 시간에는 잡음과 불규칙성에 대하여 이야기 해보도록 하겠습니다.
'R > RSTAT101' 카테고리의 다른 글
| [RSTAT101] 10강. 기초 통계분포 - 정규분포 갓벽 정리 (1) | 2023.06.10 |
|---|---|
| [RSTAT101] 9강. 잡음과 정규분포에 대하여 (0) | 2023.06.10 |
| [RSTAT101] 7강. R에서 회귀분석 실행하기 (2) | 2023.06.10 |
| [RSTAT101] 6강. 회귀직선의 의미와 구하는 방법 (0) | 2023.06.10 |
| [RSTAT101] 5강. 상관계수의 의미와 시각화 (0) | 2023.06.10 |




댓글