상관 계수(correlation coefficient)
두 개의 변수의 값을 관찰하고 있다고 생각합시다. 예를 들어 우리가 이제까지 사용했던 데이터에서 중간고사 점수과 기말고사 점수를 생각해보죠. 이 점수들을 쌍으로 묶으면, \((x_i, y_i)\)라고 생각 할 수 있고, \(i = 1, ..., n\) 명의 학생들의 점수를 가지고 있다고 생각합시다. 이러한 경우 상관 계수는 다음과 같은 공식을 통해 계산 할 수 있습니다.
\[ r=\frac{1}{n-1}\sum_{i=1}^{n}\left(\frac{x_{i}-\bar{x}}{s_{x}}\right)\left(\frac{y_{i}-\bar{y}}{s_{y}}\right) \] 위의 공식에서 \(\bar{x}, \bar{y}\)와 \(s_x, s_y\)는 중간, 기말고사 점수의 표본 평균값과 표본 표준편차를 각각 나타냅니다.
상관계수를 생각할 경우 우리가 알고 넘어가야 할 내용들은 다음과 같습니다.
- 상관계수는 두 변수의 선형적인 관계를 측정하는 지표이다.
- \(r\)은 언제나 \(-1\)에서 \(1\)사이의 값을 갖는다.
- \(r>0\) 인 경우는 양의 상관성을, \(r<0\) 인 경우는 음의 상관성을, 마지막으로 \(r=0\)인 경우는 선형 상관성이 존재하지 않는 것을 나타낸다.
- \(r=0\) 은 두 변수사이의 관계가 존재하지 않는 다는 것을 의미하는 것이 아닙니다. 선형 상관이 아닌 다른 여러가지 상관성이 존재하죠.
- 상관계수는 단위가 존재하지 않습니다.
위키피디아의 상관계수의 값에 따른 변화를 그려놓은 그림은 상관계수를 이해하는데 아주 도움이 많이 됩니다.
R에서 상관 계수 구하기 (correlation coefficient)
mydata <- read.csv("examscore.csv", header = TRUE)R에서는 cor이라는 함수를 상관계수를 구할 때 사용할 수 있습니다.
my_corr <- cor(mydata$midterm, mydata$final)
my_corr>> [1] 0.6770075cor함수가 정말 위의 공식을 사용해서 값을 구하는지 확인해 보기 위하여, 배운 공식을 그대로 사용하여 상관계수를 구해보면 다음과 같습니다.
n <- length(mydata$midterm)
x_bar <- mean(mydata$midterm)
y_bar <- mean(mydata$final)
s_x <- sd(mydata$midterm)
s_y <- sd(mydata$final)
z_x <- (mydata$midterm - x_bar) / s_x
z_y <- (mydata$final - y_bar) / s_y
sum(z_x * z_y) / (n - 1)>> [1] 0.6770075우리가 week 2에서 배운 시각화를 통하여 두 변수의 분포를 시각화 시켜보자.
plot(mydata$midterm, mydata$final, asp = 1,
xlab = "중간고사",
ylab = "기말고사",
main = "시험점수 산점도")
title(sub = paste("상관계수: ", round(my_corr, 4)), adj = 1, col.sub = "red")
abline(v = x_bar)
abline(h = y_bar)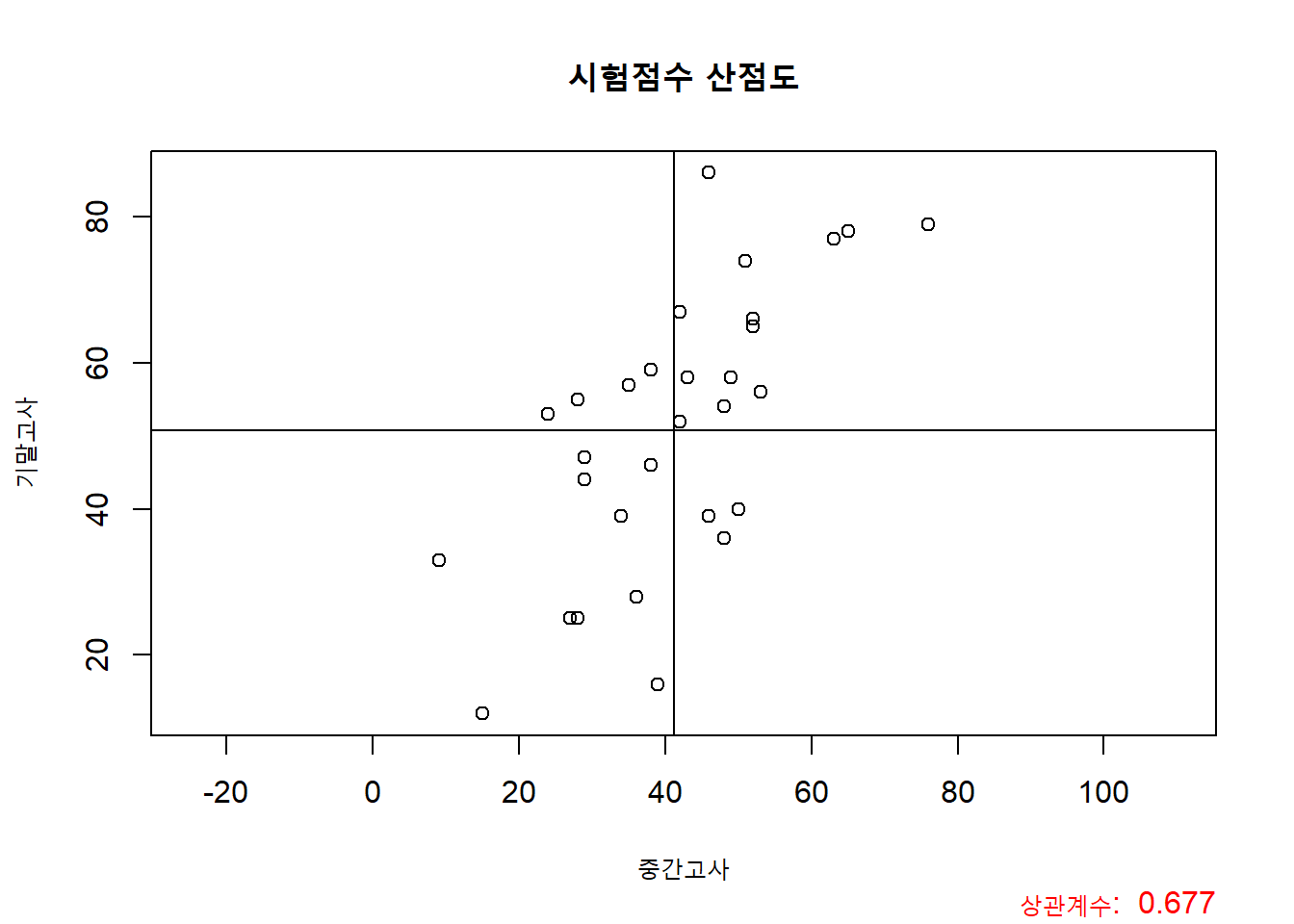
두 변수의 분포가 우상향하는 것을 알 수 있고, 이러한 분포는 상관계수값 0.6과 상응하는 것입니다. 또한, 중간고사 점수의 평균과 기말고사의 평균을 각각 수직선과 수평선으로 나타내었는데, 이것을 통해 우리는 데이터가 두 변수의 평균을 새로운 좌표축으로 생각했을때 1사분면과 3사분면에 많이 분포하고 있다는 것을 나타냅니다.
이것은 상관계수가 내포하는 의미를 좀 생각해보기 위해서 앞에서 구했던 z_x와 z_y들을 나타내보도록 하겠습니다. z_x와 z_y는 각각 중간, 기말 고사 점수를 표준화 시켰던 값들이었습니다.
plot(z_x, z_y, asp = 1,
xlab = "표준 중간고사 점수",
ylab = "표준 기말고사 점수",
main = "중간, 기말고사 표준점수 분포")
title(sub = paste("상관계수: ", round(my_corr, 4)), adj = 1, col.sub = "red")
abline(v = 0)
abline(h = 0)
위에서 살펴본 상관계수 식을 뜯어보면, 우리는 두 표준화된 점수를 곱한 값을 더해서 나줘주는 것을 알 수 있죠. 우리가 1, 2, 3, 4 사분면에 위치한 점들의 \(x, y\) 값을 곱한 값을 생각했을 경우, 1, 3 사분면에 위치한 점들은 양수가, 2, 4 사분면에 위치한 점들은 음수가 나올 것입니다. 다음과 같이 말이죠.
z_x * z_y>> [1] 0.055356131 0.049164984 0.224095213 0.079635135 -0.207706885
>> [6] 0.830827538 -0.368312500 0.048072429 1.237136681 -0.094566723
>> [11] -0.347432556 0.301302447 1.331096429 0.429010012 0.168374897
>> [16] 0.307979174 -0.139240092 0.619600198 0.274595542 2.085202312
>> [21] 3.577389937 3.697449615 2.083259992 -0.201394343 0.205400379
>> [26] 0.003641851 -0.137540561 0.599691414 2.360890410 0.560238032sign 함수를 이용하여 이 수들의 부호만 따로 정리를 해보도록 하겠습니다.
sign(z_x * z_y)>> [1] 1 1 1 1 -1 1 -1 1 1 -1 -1 1 1 1 1 1 -1 1 1 1 1 1 1 -1 1
>> [26] 1 -1 1 1 1이 부호를 이용하면 다음과 같은 그래프가 완성됩니다.
plot(z_x, z_y, asp = 1,
xlab = "표준 중간고사 점수",
ylab = "표준 기말고사 점수",
main = "중간, 기말고사 표준점수 분포",
col = c("blue", "red")[as.factor(sign(z_x * z_y))])
title(sub = paste("상관계수: ", round(my_corr, 4)), adj = 1, col.sub = "red")
abline(v = 0)
abline(h = 0)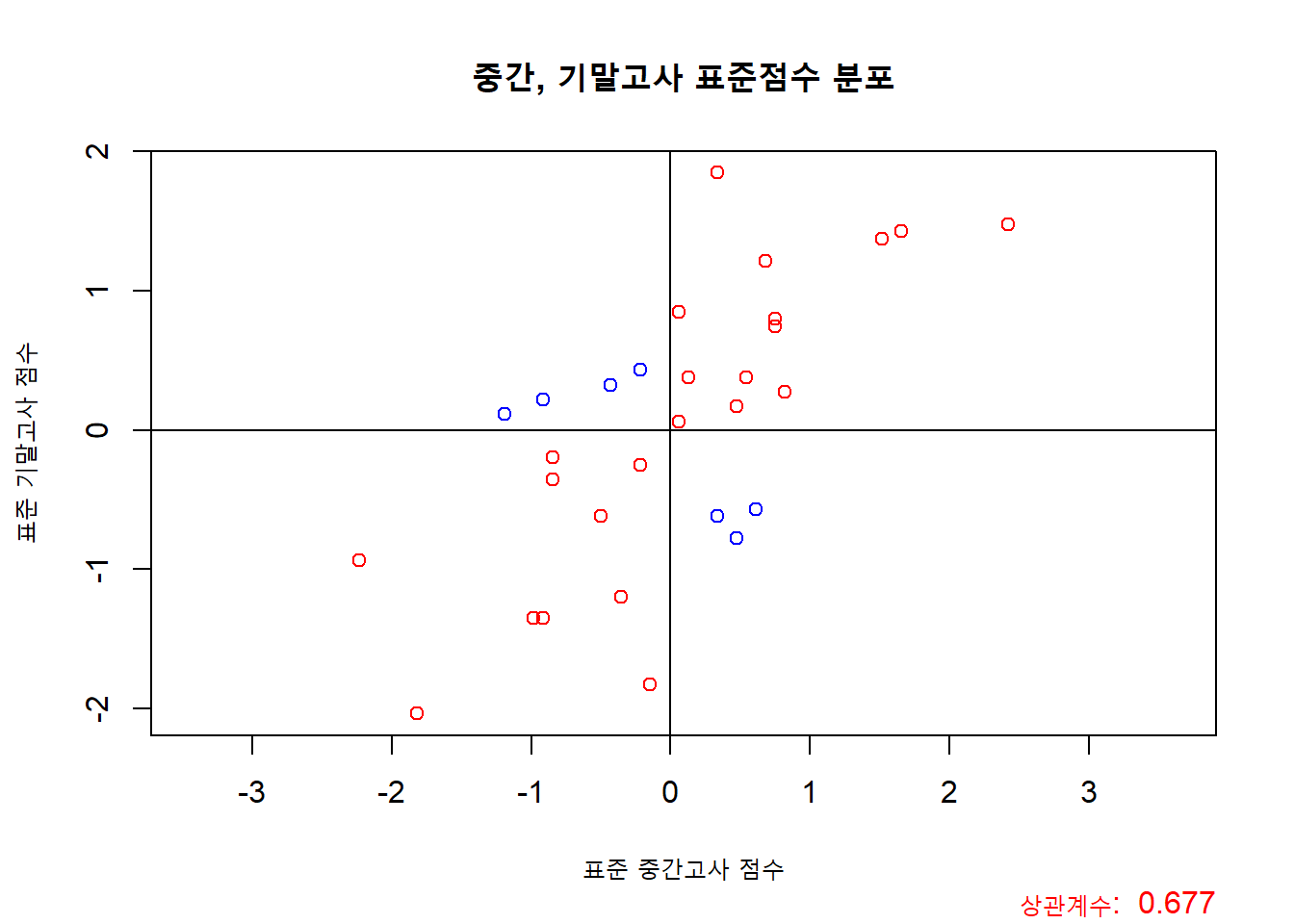
즉, 위의 그래프에서 빨간 점들은 양의 상관관계가 나오도록 도와주는(?) 데이터들이고, 파란 점들은 음의 상관관계가 나오도록 도와주는 데이터 들이라고 생각하면 좋습니다. 하지만, 부호만이 이렇게 상관관계에 영향을 미칠까요? 아닙니다. 한가지 요소가 더 있습니다. 바로 표준 점수들의 곱의 절대값 크기죠!
abs(z_x * z_y)>> [1] 0.055356131 0.049164984 0.224095213 0.079635135 0.207706885 0.830827538
>> [7] 0.368312500 0.048072429 1.237136681 0.094566723 0.347432556 0.301302447
>> [13] 1.331096429 0.429010012 0.168374897 0.307979174 0.139240092 0.619600198
>> [19] 0.274595542 2.085202312 3.577389937 3.697449615 2.083259992 0.201394343
>> [25] 0.205400379 0.003641851 0.137540561 0.599691414 2.360890410 0.560238032이 값을 점의 크기로 대체하여 봅시다.
plot(z_x, z_y, asp = 1,
xlab = "표준 중간고사 점수",
ylab = "표준 기말고사 점수",
main = "중간, 기말고사 표준점수 분포",
col = c("blue", "red")[as.factor(sign(z_x * z_y))],
cex = abs(z_x * z_y))
title(sub = paste("상관계수: ", round(my_corr, 4)), adj = 1, col.sub = "red")
abline(v = 0)
abline(h = 0)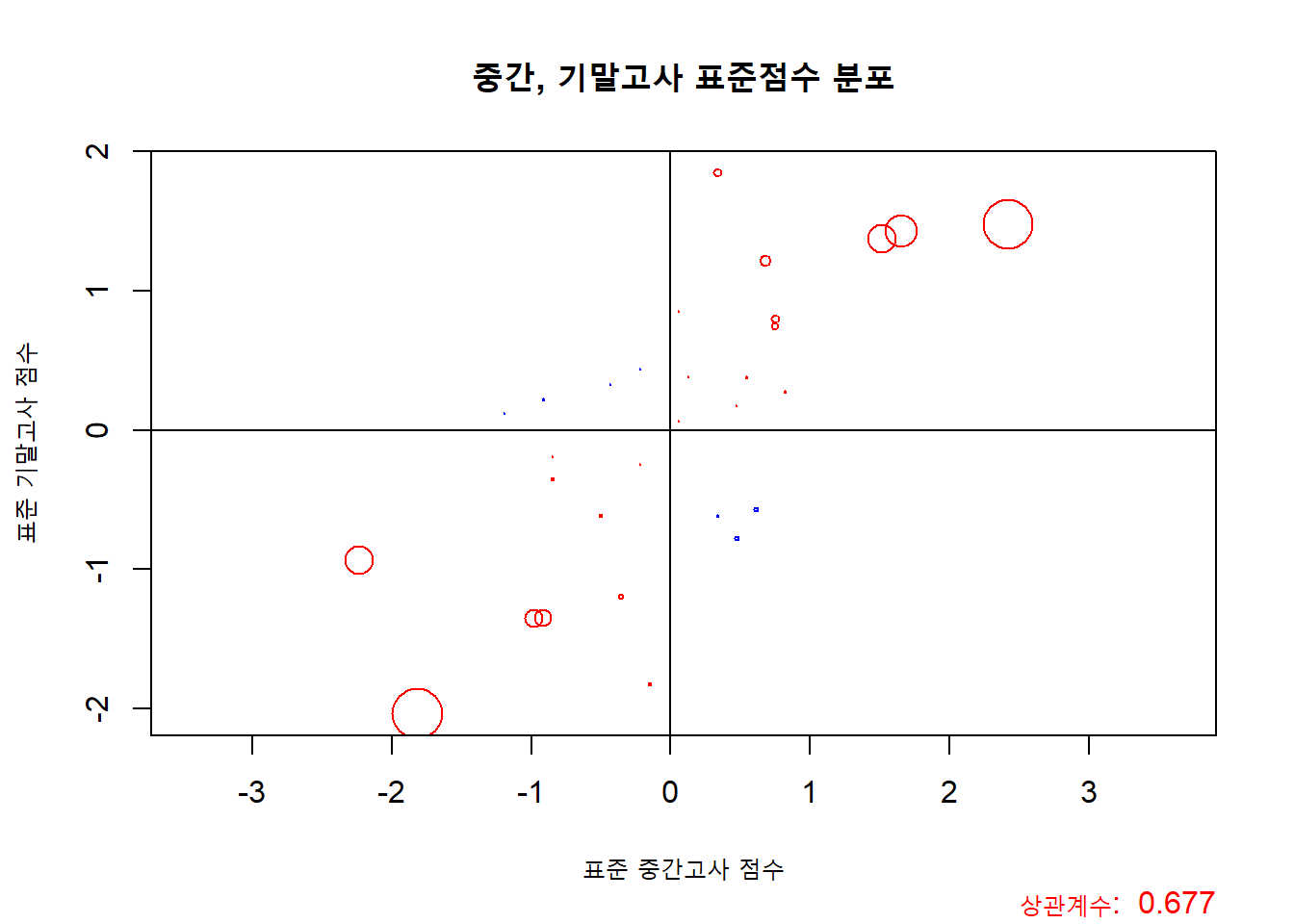
위의 그래프는 상관계수의 계산 과정을 시각화 한 그래프라고 생각하면 좋을것 같습니다. 상관계수는 그래프의 모든 점들을 더 한 후에 데이터의 개수 (-1) 만큼 나눠준 값이니까요. 값을 보면, 빨간 큰 점들이 많이 보이니, 당연히 작은 파란색 점들의 상관계수에 대한 영향력은 줄어 들 것입니다. 오늘은 여기까지 하도록 하겠습니다. 감사합니다.
'R > RSTAT101' 카테고리의 다른 글
| [RSTAT101] 7강. R에서 회귀분석 실행하기 (2) | 2023.06.10 |
|---|---|
| [RSTAT101] 6강. 회귀직선의 의미와 구하는 방법 (0) | 2023.06.10 |
| [RSTAT101] 4강. 사용자 정의함수와 최빈값 (0) | 2023.06.10 |
| [RSTAT101] 3강. 평균과 중앙값, 분산과 IQR의 관계 이해하기 (1) | 2023.06.10 |
| [RSTAT101] 2강. 기초통계 그래프들 - 파이차트, 줄기-잎 그래프, 히스토그램, 상자그림 (0) | 2023.06.09 |




댓글