이전 포스팅에서는 EM 알고리즘에 대하여 간략한 예제를 통하여 알아보았다. 이번 포스팅에서는 EM 알고리즘이 작동하는 원리에 대하여 살짝 이해해보는 시간을 갖도록 하자. 전 포스팅에서 알아보았듯, 결국 EM 알고리즘은 E step과 M step을 반복 함으로써 우도 함수를 최대화시키는 방법이다. 자연스럽게 떠오르는 질문은 ‘항상 이러한 방법을 사용하면 우도 함수를 최대로 만드는 모수를 찾을 수 있을까?’ 일 것이다. 이러한 질문의 완벽한 대답은 되지 않지만, EM 알고리즘의 Path는 이번 포스팅에서 다룰 아주 좋은 성질을 가지고 있다.
Ascent property of EM algorithm
EM 알고리즘을 사용해서 우리는 모수의 값을 계속 업데이트 해 나아간다. 이렇게 업데이트된 모수는 우리가 최대화하고 싶어 하는 로그 우도 함수의 값을 계속해서 상승시키는 좋은 성질을 가지게 되는데, 이것을 ascent property라고 한다.
예를 들어, 확률변수 \(Y\)에서부터 관찰된 데이더 \(y\)를 기반으로 정의된 로그 우도함수, \(\ell\), 을 다음과 같이 정의하자.
\[ \ell_{\theta}\left(y\right)=log\,g_{\theta}\left(y\right) \]
여기서 \(g\)는 확률변수 \(Y\)의 확률밀도함수를 의미하고, \(\theta\)는 우리가 추정해야 하는 모수를 의미한다. 위에서 언급한 EM 알고리즘 모수의 ascent 특성은 다음과 같은 식을 써서 나타낼 수 있다.
\[ \tag{*} \ell_{\theta^{\left(k+1\right)}}\left(y\right)\geq\ell_{\theta^{\left(k\right)}}\left(y\right) \]
즉, 우리가 EM 알고리즘을 반복하면 반복할수록 우도 함수의 모수에 대한 함숫값이 점점 높아진다는 것이다. 많이 하면 좋고, 함숫값이 더 높아지지 않고 수렴할 때까지 EM 알고리즘을 하면 된다는 말씀. 자, 이제 위에서 언급한 특성이 왜 발생하는지에 대하여 알아보자.
Q와 H 함수를 이용한 로그우도함수 나타내기
앞선 포스팅에서 EM 알고리즘을 적용할 때 사용했던 확률변수 \(X\)가 다시 등장한다. 즉, 주어진 확률변수 \(Y\)를 어떤 함수 \(T\)를 사용하여, \(T(X)=Y\), 만들 수 있는 확률변수 \(X\)가 존재한다고 가정하자. 확률변수 \(X\)의 확률 밀도 함수는 \(p_{\theta}\)로 정의하자. 따라서 \(X|Y\)의 조건부 확률 밀도 함수를 \(f_\theta(x|y)\)라고 정의하면,
\[ \begin{align*} f_{\theta}\left(x|y\right) & =\frac {f_{\theta}\left(x, y\right)}{g_{\theta}\left(y\right)}\\ & =\frac {f_{\theta}\left(x, t\left(x\right)\right)}{g_{\theta}\left(y\right)}\\ & =\frac{p_{\theta}\left(x\right)}{g_{\theta}\left(y\right)} \end{align*} \]
위에서 보는 것처럼 두 확률변수의 밀도함수의 분수 꼴로 나타낼 수 있을 것을 알 수 있다. 위의 식을 \(g\)를 좌변으로 옮기고, 로그를 취해보자.
\[ \begin{align*} g_{\theta}\left(y\right) & =\frac{p_{\theta}\left(x\right)}{f_{\theta}\left(x|y\right)}\\ \tag{1} log\,g_{\theta}\left(y\right) & =log\,p_{\theta}\left(x\right)-log\,f_{\theta}\left(x|y\right) \end{align*} \]
EM 알고리즘을 사용할 때 우리는 다음과 같은 Q 함수를 사용한다.
\[ Q\left(\theta,\theta^{\left(k\right)}\right)=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right] \]
식 (1)을 잘 보면 가운데의 항이 같은 꼴을 하고 있는 것을 알 수 있다. 한가지 다른 것은 식 (1)에서는 \(x\)가 소문자이고, Q 함수에서는 \(X\)가 대문자라는 사실이다. 이것은 Q함수를 계산할 때 X는 확률변수를 의미하고, 위의 식 (1)은 변수의 관계를 생각하고 계산하였기 때문이다. 즉, 식 (1)의 \(x, y\)를 확률변수로 바꾸어도 성립한다는 말이다.
Q함수와 같은 꼴을 만들기 위해 식 (1)의 모든 변수를 확률변수로 바꾸고, 양변에 EM 알고리즘의 E-step에서 사용하는 조건부 기댓값, \(\mathbb{E}\left[.|Y=y,\theta^{\left(k\right)}\right]\),을 적용하면 다음과 같다.
\[\begin{align*} & \mathbb{E}\left[log\,g_{\theta}\left(Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ = & \mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right]-\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ \Rightarrow & log\,g_{\theta}\left(y\right)=Q\left(\theta,\theta^{\left(k\right)}\right)-H\left(\theta,\theta^{\left(k\right)}\right)\\ where\, & Q\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right],\\ & H\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]. \end{align*}\]
조건부 기댓값에 \(\theta\)도 여러 개가 나오니 어려울 수 있다. 이러한 어려움의 근본적인 이유는 조건부 기댓값의 기호들에 대한 이해가 부족한 것에서부터 출발한다. 조건부 기댓값의 \([]\) 기호 안의 \(|\) 오른쪽에 언급되어 있는 조건들은 \(|\) 왼쪽은 확률변수들에 대한 조건을 담고 있다.
먼저, 첫 번째 항은 기본적으로 \(\theta\)와 확률변수 \(Y\)에 대한 함수에 조건부 기댓값을 취한 형태이다. 이 기댓값은 확률변수 Y를 대상으로 계산하게 된다. 하지만, 주어진 조건에서 \(Y=y\)라는 정보를 이미 우리가 알고 있으므로 이 정보를 안 이상 확률변수 Y는 더 이상 확률에 의하여 변하는 값이 아니게 된다. 따라서 이 조건부 기댓값은 그대로 \(log \ g_\theta(y)\)가 되는 것이다.
두 번째 항 역시 \(\theta\)와 확률변수 X에 대한 함수에 조건부 기댓값을 취한 형태이다. 확률변수 X는 \(Y=y\)라는 정보를 알고 있어도 여전히 불확실성이 존재하는 확률변수가 된다. 이전 포스팅의 예제를 들어 설명하면 길동의 가게에서 초콜릿 바닐라 아이스크림이 팔린 개수를 알고 있어도, 만약 초콜렛과 바닐라 아이스크림을 같은 수의 고객에게 팔았을때 초콜렛과 바닐라 아이스크림을 산 갯수를 알지는 못하는 것과 같은 이치이다. 따라서 확률변수 X에 대한 조건부 기댓값을 구해야 하는데 이때 확률변수 X의 확률 밀도 함수를 \(p_\theta^{(k)}\)로 놓고 구해야 한다. 따라서 결괏값을 \(\theta\)가 입력값인 함수 Q로 나타낼 수 있는 것이다. 같은 논리도 세 번째 항도 \(H\) 함수를 사용하여 나타내는 것이 가능하다.
부등식 증명
위의 관계를 이용해서, 우리가 이번 포스팅에서 보이고자 하는 EM 알고리즘의 monotonicity, 식 (*),를 다음과 같이 증명할 수 있다.
\[ \begin{align*} \ell_{\theta^{\left(k\right)}}\left(y\right) & =Q\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{2} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{3} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)\\ & =\ell_{\theta^{\left(k+1\right)}}\left(y\right) \end{align*} \]
자 하나씩 살펴보도록 하자. 처음의 등식은 앞에서 살펴본 로그 우도 함수의 Q와 H함수를 사용하여 나타낸 식의 \(\theta\)에 \(\theta^{(k)}\)를 대입한 것이다. 부등식 (2)가 성립하는 이유는 EM 알고리즘의 M-step의 정의에 의하여 성립한다. 왜냐하면 \(\theta^{(k+1)}\)의 정의가 \(Q\) 함수를 최대화시키는 값이기 때문이다. 마지막으로 부등식 (3)의 경우는 다음을 증명해야 한다.
\[ H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\geq H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right) \]
위의 식을 증명에는 H함수의 정의와 통계학과 경제학에서 유명한 Jensen의 부등식이 사용된다.
\[ \begin{align*} & H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ & =\mathbb{E}\left[log\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\\ \tag{4} & \leq log\left(\mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\right)\\ \tag{5} & =log\left(\int\left(\frac{f_{\theta^{\left(k+1\right)}}\left(x|y\right)}{f_{\theta^{\left(k\right)}}\left(x|y\right)}\right)f_{\theta^{\left(k\right)}}\left(x\right)dx\right)\\ \tag{6} & =log\left(\int f_{\theta^{\left(k+1\right)}}\left(x|y\right)dx\right)\\ & = 0 \end{align*} \]
위 부등식 (4)는 log 함수가 concave함수이기 때문에, Jensen의 부등식에 의하여 성립한다. 두 번째의 식 (5)는 기댓값의 정의에 의하여 성립하게 되고, 식 (6)은 확률 밀도 함수의 적분 값이 1이 되어야 하므로 성립하게 된다. 따라서 위의 부등식 (3)이 성립하게 되므로 증명이 끝나게 된다.
위의 정리는 우리가 EM 알고리즘을 반복하면 반복할수록, 얻어진 모수의 값이 반복 횟수를 적게 해서 얻어진 모수 값보다 로그 우도 함수의 값을 증가시키는 모수가 된다는 것이다. 하지만 여기서 중요한 사실은 이 성질이 우리가 발생시킨 모수가 로그우도 함수를 최대로 만드는 글로벌한 optimal값으로 수렴하는 것을 보장해주지는 않는다. 만약 로그우도 함수가 local maxima나 saddle point 같은 정상점들을 많이 가지고 있다면, 그러한 점들로 수렴한 가능성이 있다는 사실에 주의하도록 하자.
마지막 증명에 대한 이해 시각적 이해
앞선 증명 과정에서의 부등식 (4)~(6)이 성립하는 이유는 로그 안의 기댓값이 다음의 부등식을 만족하기 때문이다.
\[ \mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\leq1\,\,\,\,\,\,a.e.\,w.r.t.\,p_{\theta^{\left(k\right)}} \]
이 부등식을 엄밀하게 설명하기엔 필자의 역량이 아직 부족하다. 하지만 필자가 이해하고 범위 내에서 좀 더 구체적인 예를 들어 설명해보도록 하겠다. 위의 부등식에서 먼저 \(f(x|y)\)는 조건부 확률 밀도 함수이므로 결국 밀도 함수이다. 즉, 두 확률 밀도 함수의 분수 꼴에 입력값인 X가 들어간, likelihood ratio 확률변수의 기댓값이 되는 것이며, 조건의 \(\theta^{(k)}\)는 확률변수 X가 모수 \(\theta^{(k)}\)를 따른다는 것을 의미한다. 이 부분을 좀 더 구체적인 R코드를 들어서 설명하자.
균일 분포 \(U(\theta - 1/2, \theta + 1/2)\)를 따르는 확률변수 \(X_1\)와 \(X_2\)를 생각하자. 그리고 \(\theta^{(1)} = 0.5\), \(\theta^{(2)} = 1\)을 가정하자. 그렇다면 \(X_1\)는 균일분포 \(U(0, 1)\)을 따르고, \(X_2\)는 균일분포 \(U(0.5, 1.5)\)를 따르게 된다. 이 두 확률변수의 pdf는 다음과 같이 그릴 수 있을 것이다. 편의상 \(X_1\) 의 pdf를 \(f\), \(X_2\) 의 pdf를 \(g\)라고 하자.
파란색의 \(X_1\)의 pdf, 빨간색은 \(X_2\)의 pdf가 된다. 그렇다면 이러한 상황에서는 위에서 살펴본 likelihood ratio 함수, \(g(x)/f(x)\), 는 어떠한 모양이 될까?
1에서 1.5 사이는 f의 값이 0, g의 값이 1이 되어, 함숫값이 무한대가 되므로, 그리는 것을 생략하였다. 또한 두 pdf의 값이 0이 되는 부분은 임의로 1로 처리하였다.(이 부분의 처리는 우리의 결괏값과는 무관하다. 왜냐하면 우리가 생각하는 확률변수 \(X\)는 \(\theta^{(1)}\) 따르기 때문이다. 즉, 0에서 1 사이의 값 밖에 나오지 않는다.) 따라서 \(\theta^{(1)}\) 하에서 Likelihood ratio 확률변수의 조건부 기댓값은 다음과 같이 계산할 수 있다.
\[ \begin{align*} & \mathbb{E}\left[\frac{f_{\theta^{\left(2\right)}}\left(X\right)}{f_{\theta^{\left(1\right)}}\left(X\right)}|\theta=\theta^{\left(1\right)}\right]\\ = & \mathbb{E}\left[\frac{g\left(X\right)}{f\left(X\right)}|\theta=0.5\right]\\ = & 0\times\frac{1}{2}+1\times\frac{1}{2}\\ = & \frac{1}{2} \end{align*} \]
위와 같은 경우에 \(\theta^{(1)}\) 하에서 Likelihood의 조건부 기댓값은 분자의 pdf가 분모의 pdf와 같을 때 가장 큰 값, 1, 을 갖게 된다. 위의 경우처럼 정의역이 차이가 나는 경우가 아니더라도 이러한 현상은 똑같이 발생한다. 다음의 R코드를 참고하자.
theta <- seq(-10, 10, by = 0.1)
condEX <-function(theta){
rv_new <- function(x){dnorm(x, mean = theta) / dnorm(x, mean = 0)}
x <- rnorm(10^5, mean = 0)
x <- c(x, -x)
mean(rv_new(x))
}
result <- sapply(theta, condEX)
{
emptyPlot(xrange = c(-10, 10), yrange = c(0, 3))
title(main = "Cond. expectation of likelihood ratio under mu = 0",
xlab = "x", ylab = "f(x)/g(x)")
add_points(x = theta, y = result, col = "red", lwd=1.5)
}
위의 그래프에서 \(-5\) 와 \(5\) 근처에서 값이 튀는 이유는 난수를 뽑았는데, 극단치의 값이 많이 나와버려서 표본 평균의 값이 튀어버리는 현상 때문이다. 대략의 트렌드를 보면 1보다 작은 값을 유지하는 것을 알 수 있다. 이 주제와 관련한 좀 더 깊은 이해를 원하는 독자는 ‘contiguity’ 혹은 ’absolutely continuous’의 개념을 구글링 해보기 바란다. 이전 포스팅에서는 EM 알고리즘에 대하여 간략한 예제를 통하여 알아보았다. 이번 포스팅에서는 EM 알고리즘이 작동하는 원리에 대하여 살짝 이해해보는 시간을 갖도록 하자. 전 포스팅에서 알아보았듯, 결국 EM 알고리즘은 E step과 M step을 반복 함으로써 우도 함수를 최대화 시키는 방법이다. 자연스럽게 떠오르는 질문은 ‘항상 이러한 방법을 사용하면 우도함수를 최대로 만드는 모수를 찾을 수 있을까?’ 일 것이다. 이러한 질문의 완벽한 대답은 되지 않지만, EM 알고리즘의 Path는 이번 포스팅에서 다룰 아주 좋은 성질을 가지고 있다.
Ascent property of EM algorithm
EM 알고리즘을 사용해서 우리는 모수의 값을 계속 업데이트해 나아간다. 이렇게 업데이트된 모수는 우리가 최대화하고 싶어 하는 로그 우도 함수의 값을 계속해서 상승시키는 좋은 성질을 가지게 되는데, 이것을 ascent property라고 한다.
예를 들어, 확률변수 \(Y\)에서부터 관찰된 데이더 \(y\)를 기반으로 정의된 로그 우도 함수, \(\ell\), 을 다음과 같이 정의하자.
\[ \ell_{\theta}\left(y\right)=log\,g_{\theta}\left(y\right) \]
여기서 \(g\)는 확률변수 \(Y\)의 확률 밀도 함수를 의미하고, \(\theta\)는 우리가 추정해야 하는 모수를 의미한다. 위에서 언급한 EM 알고리즘 모수의 ascent 특성은 다음과 같은 식을 써서 나타낼 수 있다.
\[ \tag{*} \ell_{\theta^{\left(k+1\right)}}\left(y\right)\geq\ell_{\theta^{\left(k\right)}}\left(y\right) \]
즉, 우리가 EM 알고리즘을 반복하면 반복할수록 우도 함수의 모수에 대한 함숫값이 점점 높아진다는 것이다. 많이하면 좋고, 함수값이 더 높아지지 않고 수렴할 때까지 EM 알고리즘을 하면 된다는 말씀. 자, 이제 위에서 언급한 특성이 왜 발생하는지에 대하여 알아보자.
Q와 H 함수를 이용한 로그 우도 함수 나타내기
앞선 포스팅에서 EM 알고리즘을 적용할 때 사용했던 확률변수 \(X\)가 다시 등장한다. 즉, 주어진 확률변수 \(Y\)를 어떤 함수 \(T\)를 사용하여, \(T(X)=Y\), 만들 수 있는 확률변수 \(X\)가 존재한다고 가정하자. 확률변수 \(X\)의 확률 밀도 함수는 \(p_{\theta}\)로 정의하자. 따라서 \(X|Y\)의 조건부 확률 밀도 함수를 \(f_\theta(x|y)\)라고 정의하면,
\[ \begin{align*} f_{\theta}\left(x|y\right) & =\frac{f_{\theta}\left(x,y\right)}{g_{\theta}\left(y\right)}\\ & =\frac{f_{\theta}\left(x,t\left(x\right)\right)}{g_{\theta}\left(y\right)}\\ & =\frac{p_{\theta}\left(x\right)}{g_{\theta}\left(y\right)} \end{align*} \]
위에서 보는 것처럼 두 확률변수의 밀도 함수의 분수 꼴로 나타낼 수 있을 것을 알 수 있다. 위의 식을 \(g\)를 좌변으로 옮기고, 로그를 취해보자.
\[ \begin{align*} g_{\theta}\left(y\right) & =\frac{p_{\theta}\left(x\right)}{f_{\theta}\left(x|y\right)}\\ \tag{1} log\,g_{\theta}\left(y\right) & =log\,p_{\theta}\left(x\right)-log\,f_{\theta}\left(x|y\right) \end{align*} \]
EM 알고리즘을 사용할 때 우리는 다음과 같은 Q 함수를 사용한다.
\[ Q\left(\theta,\theta^{\left(k\right)}\right)=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right] \]
식 (1)을 잘 보면 가운데의 항이 같은 꼴을 하고 있는 것을 알 수 있다. 한 가지 다른 것은 식 (1)에서는 \(x\)가 소문자이고, Q 함수에서는 \(X\)가 대문자라는 사실이다. 이것은 Q함수를 계산할 때 X는 확률변수를 의미하고, 위의 식 (1)은 변수의 관계를 생각하고 계산하였기 때문이다. 즉, 식 (1)의 \(x, y\)를 확률변수로 바꾸어도 성립한다는 말이다.
Q함수와 같은 꼴을 만들기 위해 식 (1)의 모든 변수를 확률변수로 바꾸고, 양변에 EM 알고리즘의 E-step에서 사용하는 조건부 기댓값, \(\mathbb{E}\left[.|Y=y,\theta^{\left(k\right)}\right]\),을 적용하면 다음과 같다.
\[\begin{align*} & \mathbb{E}\left[log\,g_{\theta}\left(Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ = & \mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right]-\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ \Rightarrow & log\,g_{\theta}\left(y\right)=Q\left(\theta,\theta^{\left(k\right)}\right)-H\left(\theta,\theta^{\left(k\right)}\right)\\ where\, & Q\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right],\\ & H\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]. \end{align*}\]
조건부 기댓값에 \(\theta\)도 여러 개가 나오니 어려울 수 있다. 이러한 어려움의 근본적인 이유는 조건부 기댓값의 기호들에 대한 이해가 부족한 것에서부터 출발한다. 조건부 기댓값의 \([]\) 기호 안의 \(|\) 오른쪽에 언급되어 있는 조건들은 \(|\) 왼쪽은 확률변수들에 대한 조건을 담고 있다.
먼저, 첫 번째 항은 기본적으로 \(\theta\)와 확률변수 \(Y\)에 대한 함수에 조건부 기댓값을 취한 형태이다. 이 기댓값은 확률변수 Y를 대상으로 계산하게 된다. 하지만, 주어진 조건에서 \(Y=y\)라는 정보를 이미 우리가 알고 있으므로 이 정보를 안 이상 확률변수 Y는 더 이상 확률에 의하여 변하는 값이 아니게 된다. 따라서 이 조건부 기댓값은 그대로 \(log \ g_\theta(y)\)가 되는 것이다.
두 번째 항 역시 \(\theta\)와 확률변수 X에 대한 함수에 조건부 기댓값을 취한 형태이다. 확률변수 X는 \(Y=y\)라는 정보를 알고 있어도 여전히 불확실성이 존재하는 확률변수가 된다. 이전 포스팅의 예제를 들어 설명하면 길동의 가게에서 초콜릿 바닐라 아이스크림이 팔린 개수를 알고 있어도, 만약 초콜렛과 바닐라 아이스크림을 같은 수의 고객에게 팔았을때 초콜렛과 바닐라 아이스크림을 산 갯수를 알지는 못하는 것과 같은 이치이다. 따라서 확률변수 X에 대한 조건부 기댓값을 구해야 하는데 이때 확률변수 X의 확률 밀도 함수를 \(p_\theta^{(k)}\)로 놓고 구해야 한다. 따라서 결괏값을 \(\theta\)가 입력값인 함수 Q로 나타낼 수 있는 것이다. 같은 논리도 세 번째 항도 \(H\) 함수를 사용하여 나타내는 것이 가능하다.
부등식 증명
위의 관계를 이용해서, 우리가 이번 포스팅에서 보이고자 하는 EM 알고리즘의 monotonicity, 식 (*),를 다음과 같이 증명할 수 있다.
\[ \begin{align*} \ell_{\theta^{\left(k\right)}}\left(y\right) & =Q\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{2} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{3} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)\\ & =\ell_{\theta^{\left(k+1\right)}}\left(y\right) \end{align*} \]
자 하나씩 살펴보도록 하자. 처음의 등식은 앞에서 살펴본 로그 우도 함수의 Q와 H함수를 사용하여 나타낸 식의 \(\theta\)에 \(\theta^{(k)}\)를 대입한 것이다. 부등식 (2)가 성립하는 이유는 EM 알고리즘의 M-step의 정의에 의하여 성립한다. 왜냐하면 \(\theta^{(k+1)}\)의 정의가 \(Q\) 함수를 최대화시키는 값이기 때문이다. 마지막으로 부등식 (3)의 경우는 다음을 증명해야 한다.
\[ H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\geq H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right) \]
위의 식을 증명에는 H함수의 정의와 통계학과 경제학에서 유명한 Jensen의 부등식이 사용된다.
\[ \begin{align*} & H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ & =\mathbb{E}\left[log\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\\ \tag{4} & \leq log\left(\mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\right)\\ \tag{5} & =log\left(\int\left(\frac{f_{\theta^{\left(k+1\right)}}\left(x|y\right)}{f_{\theta^{\left(k\right)}}\left(x|y\right)}\right)f_{\theta^{\left(k\right)}}\left(x\right)dx\right)\\ \tag{6} & =log\left(\int f_{\theta^{\left(k+1\right)}}\left(x|y\right)dx\right)\\ & = 0 \end{align*} \]
위 부등식 (4)는 log 함수가 concave함수이기 때문에, Jensen의 부등식에 의하여 성립한다. 두 번째의 식 (5)는 기댓값의 정의에 의하여 성립하게 되고, 식 (6)은 확률 밀도 함수의 적분 값이 1이 되어야 하므로 성립하게 된다. 따라서 위의 부등식 (3)이 성립하게 되므로 증명이 끝나게 된다.
위의 정리는 우리가 EM 알고리즘을 반복하면 반복할수록, 얻어진 모수의 값이 반복 횟수를 적게 해서 얻어진 모수 값보다 로그 우도 함수의 값을 증가시키는 모수가 된다는 것이다. 하지만 여기서 중요한 사실은 이 성질이 우리가 발생시킨 모수가 로그우도 함수를 최대로 만드는 글로벌한 optimal값으로 수렴하는 것을 보장해주지는 않는다. 만약 로그우도 함수가 local maxima나 saddle point 같은 정상점들을 많이 가지고 있다면, 그러한 점들로 수렴한 가능성이 있다는 사실에 주의하도록 하자.
마지막 증명에 대한 이해 시각적 이해
앞선 증명 과정에서의 부등식 (4)~(6)이 성립하는 이유는 로그 안의 기댓값이 다음의 부등식을 만족하기 때문이다.
\[ \mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\leq1\,\,\,\,\,\,a.e.\,w.r.t.\,p_{\theta^{\left(k\right)}} \]
이 부등식을 엄밀하게 설명하기엔 필자의 역량이 아직 부족하다. 하지만 필자가 이해하고 범위 내에서 좀 더 구체적인 예를 들어 설명해보도록 하겠다. 위의 부등식에서 먼저 \(f(x|y)\)는 조건부 확률 밀도 함수이므로 결국 밀도 함수이다. 즉, 두 확률 밀도 함수의 분수 꼴에 입력값인 X가 들어간, likelihood ratio 확률변수의 기댓값이 되는 것이며, 조건의 \(\theta^{(k)}\)는 확률변수 X가 모수 \(\theta^{(k)}\)를 따른다는 것을 의미한다. 이 부분을 좀 더 구체적인 R코드를 들어서 설명하자.
균일 분포 \(U(\theta - 1/2, \theta + 1/2)\)를 따르는 확률변수 \(X_1\)와 \(X_2\)를 생각하자. 그리고 \(\theta^{(1)} = 0.5\), \(\theta^{(2)} = 1\)을 가정하자. 그렇다면 \(X_1\)는 균일분포 \(U(0, 1)\)을 따르고, \(X_2\)는 균일분포 \(U(0.5, 1.5)\)를 따르게 된다. 이 두 확률변수의 pdf는 다음과 같이 그릴 수 있을 것이다. 편의상 \(X_1\) 의 pdf를 \(f\), \(X_2\) 의 pdf를 \(g\)라고 하자.
파란색의 \(X_1\)의 pdf, 빨간색은 \(X_2\)의 pdf가 된다. 그렇다면 이러한 상황에서는 위에서 살펴본 likelihood ratio 함수, \(g(x)/f(x)\), 는 어떠한 모양이 될까?
1에서 1.5 사이는 f의 값이 0, g의 값이 1이 되어, 함숫값이 무한대가 되므로, 그리는 것을 생략하였다. 또한 두 pdf의 값이 0이 되는 부분은 임의로 1로 처리하였다.(이 부분의 처리는 우리의 결괏값과는 무관하다. 왜냐하면 우리가 생각하는 확률변수 \(X\)는 \(\theta^{(1)}\) 따르기 때문이다. 즉, 0에서 1 사이의 값 밖에 나오지 않는다.) 따라서 \(\theta^{(1)}\) 하에서 Likelihood ratio 확률변수의 조건부 기댓값은 다음과 같이 계산할 수 있다.
\[ \begin{align*} & \mathbb{E}\left[\frac{f_{\theta^{\left(2\right)}}\left(X\right)}{f_{\theta^{\left(1\right)}}\left(X\right)}|\theta=\theta^{\left(1\right)}\right]\\ = & \mathbb{E}\left[\frac{g\left(X\right)}{f\left(X\right)}|\theta=0.5\right]\\ = & 0\times\frac{1}{2}+1\times\frac{1}{2}\\ = & \frac{1}{2} \end{align*} \]
위와 같은 경우에 \(\theta^{(1)}\) 하에서 Likelihood의 조건부 기댓값은 분자의 pdf가 분모의 pdf와 같을 때 가장 큰 값, 1, 을 갖게 된다. 위의 경우처럼 정의역이 차이가 나는 경우가 아니더라도 이러한 현상은 똑같이 발생한다. 다음의 R코드를 참고하자.
theta <- seq(-10, 10, by = 0.1)
condEX <-function(theta){
rv_new <-function(x){dnorm(x, mean = theta) / dnorm(x, mean = 0)}
x <- rnorm(10^5, mean = 0)
x <- c(x, -x)
result <- sapply(theta, condEX)
{
emptyPlot(xrange = c(-10, 10), yrange = c(0, 3))
title(main = "Cond. expectation of likelihood ratio under mu = 0",
xlab = "x", ylab = "f(x)/g(x)")
add_points(x = theta, y = result, col = "red", lwd=1.5)
}
위의 그래프에서 \(-5\) 와 \(5\) 근처에서 값이 튀는 이유는 난수를 뽑았는데, 극단치의 값이 많이 나와버려서 표본 평균의 값이 튀어버리는 현상 때문이다. 대략의 트렌드를 보면 1보다 작은 값을 유지하는 것을 알 수 있다. 이 주제와 관련한 좀 더 깊은 이해를 원하는 독자는 ‘contiguity’ 혹은 ’absolutely continuous’의 개념을 구글링 해보기 바란다.
Reference
[1] Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. New York: Springer series in statistics, 2001.
[2] Huang, Jian. The University of Iowa, Advanced Inference I lecture note.
Ascent property of EM algorithm
EM 알고리즘을 사용해서 우리는 모수의 값을 계속 업데이트 해 나아간다. 이렇게 업데이트된 모수는 우리가 최대화하고 싶어 하는 로그 우도 함수의 값을 계속해서 상승시키는 좋은 성질을 가지게 되는데, 이것을 ascent property라고 한다.
예를 들어, 확률변수 \(Y\)에서부터 관찰된 데이더 \(y\)를 기반으로 정의된 로그 우도함수, \(\ell\), 을 다음과 같이 정의하자.
\[ \ell_{\theta}\left(y\right)=log\,g_{\theta}\left(y\right) \]
여기서 \(g\)는 확률변수 \(Y\)의 확률밀도함수를 의미하고, \(\theta\)는 우리가 추정해야 하는 모수를 의미한다. 위에서 언급한 EM 알고리즘 모수의 ascent 특성은 다음과 같은 식을 써서 나타낼 수 있다.
\[ \tag{*} \ell_{\theta^{\left(k+1\right)}}\left(y\right)\geq\ell_{\theta^{\left(k\right)}}\left(y\right) \]
즉, 우리가 EM 알고리즘을 반복하면 반복할수록 우도 함수의 모수에 대한 함숫값이 점점 높아진다는 것이다. 많이 하면 좋고, 함숫값이 더 높아지지 않고 수렴할 때까지 EM 알고리즘을 하면 된다는 말씀. 자, 이제 위에서 언급한 특성이 왜 발생하는지에 대하여 알아보자.
Q와 H 함수를 이용한 로그우도함수 나타내기
앞선 포스팅에서 EM 알고리즘을 적용할 때 사용했던 확률변수 \(X\)가 다시 등장한다. 즉, 주어진 확률변수 \(Y\)를 어떤 함수 \(T\)를 사용하여, \(T(X)=Y\), 만들 수 있는 확률변수 \(X\)가 존재한다고 가정하자. 확률변수 \(X\)의 확률 밀도 함수는 \(p_{\theta}\)로 정의하자. 따라서 \(X|Y\)의 조건부 확률 밀도 함수를 \(f_\theta(x|y)\)라고 정의하면,
\[ \begin{align*} f_{\theta}\left(x|y\right) & =\frac {f_{\theta}\left(x, y\right)}{g_{\theta}\left(y\right)}\\ & =\frac {f_{\theta}\left(x, t\left(x\right)\right)}{g_{\theta}\left(y\right)}\\ & =\frac{p_{\theta}\left(x\right)}{g_{\theta}\left(y\right)} \end{align*} \]
위에서 보는 것처럼 두 확률변수의 밀도함수의 분수 꼴로 나타낼 수 있을 것을 알 수 있다. 위의 식을 \(g\)를 좌변으로 옮기고, 로그를 취해보자.
\[ \begin{align*} g_{\theta}\left(y\right) & =\frac{p_{\theta}\left(x\right)}{f_{\theta}\left(x|y\right)}\\ \tag{1} log\,g_{\theta}\left(y\right) & =log\,p_{\theta}\left(x\right)-log\,f_{\theta}\left(x|y\right) \end{align*} \]
EM 알고리즘을 사용할 때 우리는 다음과 같은 Q 함수를 사용한다.
\[ Q\left(\theta,\theta^{\left(k\right)}\right)=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right] \]
식 (1)을 잘 보면 가운데의 항이 같은 꼴을 하고 있는 것을 알 수 있다. 한가지 다른 것은 식 (1)에서는 \(x\)가 소문자이고, Q 함수에서는 \(X\)가 대문자라는 사실이다. 이것은 Q함수를 계산할 때 X는 확률변수를 의미하고, 위의 식 (1)은 변수의 관계를 생각하고 계산하였기 때문이다. 즉, 식 (1)의 \(x, y\)를 확률변수로 바꾸어도 성립한다는 말이다.
Q함수와 같은 꼴을 만들기 위해 식 (1)의 모든 변수를 확률변수로 바꾸고, 양변에 EM 알고리즘의 E-step에서 사용하는 조건부 기댓값, \(\mathbb{E}\left[.|Y=y,\theta^{\left(k\right)}\right]\),을 적용하면 다음과 같다.
\[\begin{align*} & \mathbb{E}\left[log\,g_{\theta}\left(Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ = & \mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right]-\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ \Rightarrow & log\,g_{\theta}\left(y\right)=Q\left(\theta,\theta^{\left(k\right)}\right)-H\left(\theta,\theta^{\left(k\right)}\right)\\ where\, & Q\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right],\\ & H\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]. \end{align*}\]
조건부 기댓값에 \(\theta\)도 여러 개가 나오니 어려울 수 있다. 이러한 어려움의 근본적인 이유는 조건부 기댓값의 기호들에 대한 이해가 부족한 것에서부터 출발한다. 조건부 기댓값의 \([]\) 기호 안의 \(|\) 오른쪽에 언급되어 있는 조건들은 \(|\) 왼쪽은 확률변수들에 대한 조건을 담고 있다.
먼저, 첫 번째 항은 기본적으로 \(\theta\)와 확률변수 \(Y\)에 대한 함수에 조건부 기댓값을 취한 형태이다. 이 기댓값은 확률변수 Y를 대상으로 계산하게 된다. 하지만, 주어진 조건에서 \(Y=y\)라는 정보를 이미 우리가 알고 있으므로 이 정보를 안 이상 확률변수 Y는 더 이상 확률에 의하여 변하는 값이 아니게 된다. 따라서 이 조건부 기댓값은 그대로 \(log \ g_\theta(y)\)가 되는 것이다.
두 번째 항 역시 \(\theta\)와 확률변수 X에 대한 함수에 조건부 기댓값을 취한 형태이다. 확률변수 X는 \(Y=y\)라는 정보를 알고 있어도 여전히 불확실성이 존재하는 확률변수가 된다. 이전 포스팅의 예제를 들어 설명하면 길동의 가게에서 초콜릿 바닐라 아이스크림이 팔린 개수를 알고 있어도, 만약 초콜렛과 바닐라 아이스크림을 같은 수의 고객에게 팔았을때 초콜렛과 바닐라 아이스크림을 산 갯수를 알지는 못하는 것과 같은 이치이다. 따라서 확률변수 X에 대한 조건부 기댓값을 구해야 하는데 이때 확률변수 X의 확률 밀도 함수를 \(p_\theta^{(k)}\)로 놓고 구해야 한다. 따라서 결괏값을 \(\theta\)가 입력값인 함수 Q로 나타낼 수 있는 것이다. 같은 논리도 세 번째 항도 \(H\) 함수를 사용하여 나타내는 것이 가능하다.
부등식 증명
위의 관계를 이용해서, 우리가 이번 포스팅에서 보이고자 하는 EM 알고리즘의 monotonicity, 식 (*),를 다음과 같이 증명할 수 있다.
\[ \begin{align*} \ell_{\theta^{\left(k\right)}}\left(y\right) & =Q\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{2} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{3} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)\\ & =\ell_{\theta^{\left(k+1\right)}}\left(y\right) \end{align*} \]
자 하나씩 살펴보도록 하자. 처음의 등식은 앞에서 살펴본 로그 우도 함수의 Q와 H함수를 사용하여 나타낸 식의 \(\theta\)에 \(\theta^{(k)}\)를 대입한 것이다. 부등식 (2)가 성립하는 이유는 EM 알고리즘의 M-step의 정의에 의하여 성립한다. 왜냐하면 \(\theta^{(k+1)}\)의 정의가 \(Q\) 함수를 최대화시키는 값이기 때문이다. 마지막으로 부등식 (3)의 경우는 다음을 증명해야 한다.
\[ H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\geq H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right) \]
위의 식을 증명에는 H함수의 정의와 통계학과 경제학에서 유명한 Jensen의 부등식이 사용된다.
\[ \begin{align*} & H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ & =\mathbb{E}\left[log\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\\ \tag{4} & \leq log\left(\mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\right)\\ \tag{5} & =log\left(\int\left(\frac{f_{\theta^{\left(k+1\right)}}\left(x|y\right)}{f_{\theta^{\left(k\right)}}\left(x|y\right)}\right)f_{\theta^{\left(k\right)}}\left(x\right)dx\right)\\ \tag{6} & =log\left(\int f_{\theta^{\left(k+1\right)}}\left(x|y\right)dx\right)\\ & = 0 \end{align*} \]
위 부등식 (4)는 log 함수가 concave함수이기 때문에, Jensen의 부등식에 의하여 성립한다. 두 번째의 식 (5)는 기댓값의 정의에 의하여 성립하게 되고, 식 (6)은 확률 밀도 함수의 적분 값이 1이 되어야 하므로 성립하게 된다. 따라서 위의 부등식 (3)이 성립하게 되므로 증명이 끝나게 된다.
위의 정리는 우리가 EM 알고리즘을 반복하면 반복할수록, 얻어진 모수의 값이 반복 횟수를 적게 해서 얻어진 모수 값보다 로그 우도 함수의 값을 증가시키는 모수가 된다는 것이다. 하지만 여기서 중요한 사실은 이 성질이 우리가 발생시킨 모수가 로그우도 함수를 최대로 만드는 글로벌한 optimal값으로 수렴하는 것을 보장해주지는 않는다. 만약 로그우도 함수가 local maxima나 saddle point 같은 정상점들을 많이 가지고 있다면, 그러한 점들로 수렴한 가능성이 있다는 사실에 주의하도록 하자.
마지막 증명에 대한 이해 시각적 이해
앞선 증명 과정에서의 부등식 (4)~(6)이 성립하는 이유는 로그 안의 기댓값이 다음의 부등식을 만족하기 때문이다.
\[ \mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\leq1\,\,\,\,\,\,a.e.\,w.r.t.\,p_{\theta^{\left(k\right)}} \]
이 부등식을 엄밀하게 설명하기엔 필자의 역량이 아직 부족하다. 하지만 필자가 이해하고 범위 내에서 좀 더 구체적인 예를 들어 설명해보도록 하겠다. 위의 부등식에서 먼저 \(f(x|y)\)는 조건부 확률 밀도 함수이므로 결국 밀도 함수이다. 즉, 두 확률 밀도 함수의 분수 꼴에 입력값인 X가 들어간, likelihood ratio 확률변수의 기댓값이 되는 것이며, 조건의 \(\theta^{(k)}\)는 확률변수 X가 모수 \(\theta^{(k)}\)를 따른다는 것을 의미한다. 이 부분을 좀 더 구체적인 R코드를 들어서 설명하자.
균일 분포 \(U(\theta - 1/2, \theta + 1/2)\)를 따르는 확률변수 \(X_1\)와 \(X_2\)를 생각하자. 그리고 \(\theta^{(1)} = 0.5\), \(\theta^{(2)} = 1\)을 가정하자. 그렇다면 \(X_1\)는 균일분포 \(U(0, 1)\)을 따르고, \(X_2\)는 균일분포 \(U(0.5, 1.5)\)를 따르게 된다. 이 두 확률변수의 pdf는 다음과 같이 그릴 수 있을 것이다. 편의상 \(X_1\) 의 pdf를 \(f\), \(X_2\) 의 pdf를 \(g\)라고 하자.
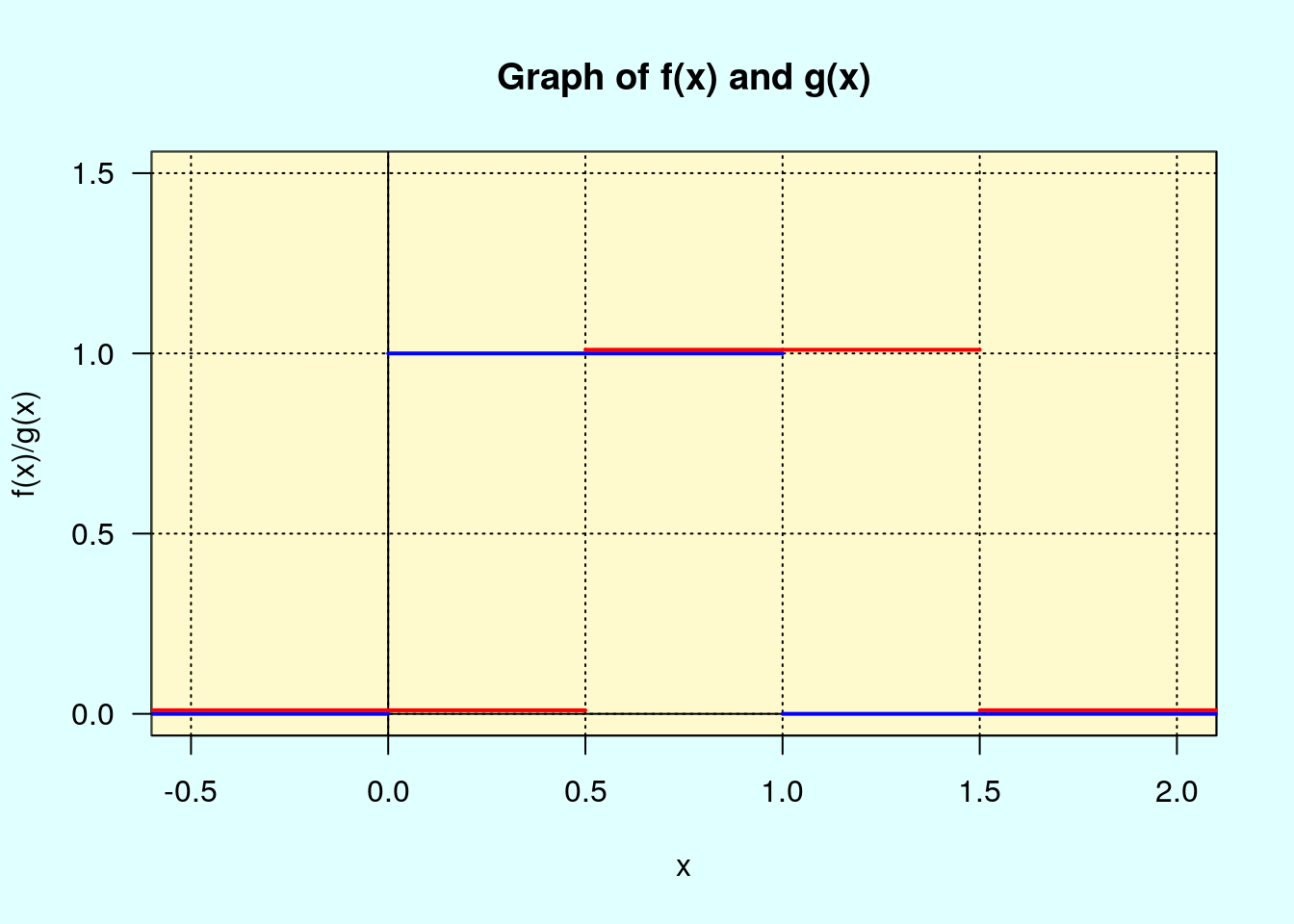
파란색의 \(X_1\)의 pdf, 빨간색은 \(X_2\)의 pdf가 된다. 그렇다면 이러한 상황에서는 위에서 살펴본 likelihood ratio 함수, \(g(x)/f(x)\), 는 어떠한 모양이 될까?

1에서 1.5 사이는 f의 값이 0, g의 값이 1이 되어, 함숫값이 무한대가 되므로, 그리는 것을 생략하였다. 또한 두 pdf의 값이 0이 되는 부분은 임의로 1로 처리하였다.(이 부분의 처리는 우리의 결괏값과는 무관하다. 왜냐하면 우리가 생각하는 확률변수 \(X\)는 \(\theta^{(1)}\) 따르기 때문이다. 즉, 0에서 1 사이의 값 밖에 나오지 않는다.) 따라서 \(\theta^{(1)}\) 하에서 Likelihood ratio 확률변수의 조건부 기댓값은 다음과 같이 계산할 수 있다.
\[ \begin{align*} & \mathbb{E}\left[\frac{f_{\theta^{\left(2\right)}}\left(X\right)}{f_{\theta^{\left(1\right)}}\left(X\right)}|\theta=\theta^{\left(1\right)}\right]\\ = & \mathbb{E}\left[\frac{g\left(X\right)}{f\left(X\right)}|\theta=0.5\right]\\ = & 0\times\frac{1}{2}+1\times\frac{1}{2}\\ = & \frac{1}{2} \end{align*} \]
위와 같은 경우에 \(\theta^{(1)}\) 하에서 Likelihood의 조건부 기댓값은 분자의 pdf가 분모의 pdf와 같을 때 가장 큰 값, 1, 을 갖게 된다. 위의 경우처럼 정의역이 차이가 나는 경우가 아니더라도 이러한 현상은 똑같이 발생한다. 다음의 R코드를 참고하자.
theta <- seq(-10, 10, by = 0.1)
condEX <-function(theta){
rv_new <- function(x){dnorm(x, mean = theta) / dnorm(x, mean = 0)}
x <- rnorm(10^5, mean = 0)
x <- c(x, -x)
mean(rv_new(x))
}
result <- sapply(theta, condEX)
{
emptyPlot(xrange = c(-10, 10), yrange = c(0, 3))
title(main = "Cond. expectation of likelihood ratio under mu = 0",
xlab = "x", ylab = "f(x)/g(x)")
add_points(x = theta, y = result, col = "red", lwd=1.5)
}
위의 그래프에서 \(-5\) 와 \(5\) 근처에서 값이 튀는 이유는 난수를 뽑았는데, 극단치의 값이 많이 나와버려서 표본 평균의 값이 튀어버리는 현상 때문이다. 대략의 트렌드를 보면 1보다 작은 값을 유지하는 것을 알 수 있다. 이 주제와 관련한 좀 더 깊은 이해를 원하는 독자는 ‘contiguity’ 혹은 ’absolutely continuous’의 개념을 구글링 해보기 바란다. 이전 포스팅에서는 EM 알고리즘에 대하여 간략한 예제를 통하여 알아보았다. 이번 포스팅에서는 EM 알고리즘이 작동하는 원리에 대하여 살짝 이해해보는 시간을 갖도록 하자. 전 포스팅에서 알아보았듯, 결국 EM 알고리즘은 E step과 M step을 반복 함으로써 우도 함수를 최대화 시키는 방법이다. 자연스럽게 떠오르는 질문은 ‘항상 이러한 방법을 사용하면 우도함수를 최대로 만드는 모수를 찾을 수 있을까?’ 일 것이다. 이러한 질문의 완벽한 대답은 되지 않지만, EM 알고리즘의 Path는 이번 포스팅에서 다룰 아주 좋은 성질을 가지고 있다.
Ascent property of EM algorithm
EM 알고리즘을 사용해서 우리는 모수의 값을 계속 업데이트해 나아간다. 이렇게 업데이트된 모수는 우리가 최대화하고 싶어 하는 로그 우도 함수의 값을 계속해서 상승시키는 좋은 성질을 가지게 되는데, 이것을 ascent property라고 한다.
예를 들어, 확률변수 \(Y\)에서부터 관찰된 데이더 \(y\)를 기반으로 정의된 로그 우도 함수, \(\ell\), 을 다음과 같이 정의하자.
\[ \ell_{\theta}\left(y\right)=log\,g_{\theta}\left(y\right) \]
여기서 \(g\)는 확률변수 \(Y\)의 확률 밀도 함수를 의미하고, \(\theta\)는 우리가 추정해야 하는 모수를 의미한다. 위에서 언급한 EM 알고리즘 모수의 ascent 특성은 다음과 같은 식을 써서 나타낼 수 있다.
\[ \tag{*} \ell_{\theta^{\left(k+1\right)}}\left(y\right)\geq\ell_{\theta^{\left(k\right)}}\left(y\right) \]
즉, 우리가 EM 알고리즘을 반복하면 반복할수록 우도 함수의 모수에 대한 함숫값이 점점 높아진다는 것이다. 많이하면 좋고, 함수값이 더 높아지지 않고 수렴할 때까지 EM 알고리즘을 하면 된다는 말씀. 자, 이제 위에서 언급한 특성이 왜 발생하는지에 대하여 알아보자.
Q와 H 함수를 이용한 로그 우도 함수 나타내기
앞선 포스팅에서 EM 알고리즘을 적용할 때 사용했던 확률변수 \(X\)가 다시 등장한다. 즉, 주어진 확률변수 \(Y\)를 어떤 함수 \(T\)를 사용하여, \(T(X)=Y\), 만들 수 있는 확률변수 \(X\)가 존재한다고 가정하자. 확률변수 \(X\)의 확률 밀도 함수는 \(p_{\theta}\)로 정의하자. 따라서 \(X|Y\)의 조건부 확률 밀도 함수를 \(f_\theta(x|y)\)라고 정의하면,
\[ \begin{align*} f_{\theta}\left(x|y\right) & =\frac{f_{\theta}\left(x,y\right)}{g_{\theta}\left(y\right)}\\ & =\frac{f_{\theta}\left(x,t\left(x\right)\right)}{g_{\theta}\left(y\right)}\\ & =\frac{p_{\theta}\left(x\right)}{g_{\theta}\left(y\right)} \end{align*} \]
위에서 보는 것처럼 두 확률변수의 밀도 함수의 분수 꼴로 나타낼 수 있을 것을 알 수 있다. 위의 식을 \(g\)를 좌변으로 옮기고, 로그를 취해보자.
\[ \begin{align*} g_{\theta}\left(y\right) & =\frac{p_{\theta}\left(x\right)}{f_{\theta}\left(x|y\right)}\\ \tag{1} log\,g_{\theta}\left(y\right) & =log\,p_{\theta}\left(x\right)-log\,f_{\theta}\left(x|y\right) \end{align*} \]
EM 알고리즘을 사용할 때 우리는 다음과 같은 Q 함수를 사용한다.
\[ Q\left(\theta,\theta^{\left(k\right)}\right)=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right] \]
식 (1)을 잘 보면 가운데의 항이 같은 꼴을 하고 있는 것을 알 수 있다. 한 가지 다른 것은 식 (1)에서는 \(x\)가 소문자이고, Q 함수에서는 \(X\)가 대문자라는 사실이다. 이것은 Q함수를 계산할 때 X는 확률변수를 의미하고, 위의 식 (1)은 변수의 관계를 생각하고 계산하였기 때문이다. 즉, 식 (1)의 \(x, y\)를 확률변수로 바꾸어도 성립한다는 말이다.
Q함수와 같은 꼴을 만들기 위해 식 (1)의 모든 변수를 확률변수로 바꾸고, 양변에 EM 알고리즘의 E-step에서 사용하는 조건부 기댓값, \(\mathbb{E}\left[.|Y=y,\theta^{\left(k\right)}\right]\),을 적용하면 다음과 같다.
\[\begin{align*} & \mathbb{E}\left[log\,g_{\theta}\left(Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ = & \mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right]-\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]\\ \Rightarrow & log\,g_{\theta}\left(y\right)=Q\left(\theta,\theta^{\left(k\right)}\right)-H\left(\theta,\theta^{\left(k\right)}\right)\\ where\, & Q\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,p_{\theta}\left(X\right)|Y=y,\theta^{\left(k\right)}\right],\\ & H\left(\theta,\theta^{\left(k\right)}\right):=\mathbb{E}\left[log\,f_{\theta}\left(X|Y\right)|Y=y,\theta^{\left(k\right)}\right]. \end{align*}\]
조건부 기댓값에 \(\theta\)도 여러 개가 나오니 어려울 수 있다. 이러한 어려움의 근본적인 이유는 조건부 기댓값의 기호들에 대한 이해가 부족한 것에서부터 출발한다. 조건부 기댓값의 \([]\) 기호 안의 \(|\) 오른쪽에 언급되어 있는 조건들은 \(|\) 왼쪽은 확률변수들에 대한 조건을 담고 있다.
먼저, 첫 번째 항은 기본적으로 \(\theta\)와 확률변수 \(Y\)에 대한 함수에 조건부 기댓값을 취한 형태이다. 이 기댓값은 확률변수 Y를 대상으로 계산하게 된다. 하지만, 주어진 조건에서 \(Y=y\)라는 정보를 이미 우리가 알고 있으므로 이 정보를 안 이상 확률변수 Y는 더 이상 확률에 의하여 변하는 값이 아니게 된다. 따라서 이 조건부 기댓값은 그대로 \(log \ g_\theta(y)\)가 되는 것이다.
두 번째 항 역시 \(\theta\)와 확률변수 X에 대한 함수에 조건부 기댓값을 취한 형태이다. 확률변수 X는 \(Y=y\)라는 정보를 알고 있어도 여전히 불확실성이 존재하는 확률변수가 된다. 이전 포스팅의 예제를 들어 설명하면 길동의 가게에서 초콜릿 바닐라 아이스크림이 팔린 개수를 알고 있어도, 만약 초콜렛과 바닐라 아이스크림을 같은 수의 고객에게 팔았을때 초콜렛과 바닐라 아이스크림을 산 갯수를 알지는 못하는 것과 같은 이치이다. 따라서 확률변수 X에 대한 조건부 기댓값을 구해야 하는데 이때 확률변수 X의 확률 밀도 함수를 \(p_\theta^{(k)}\)로 놓고 구해야 한다. 따라서 결괏값을 \(\theta\)가 입력값인 함수 Q로 나타낼 수 있는 것이다. 같은 논리도 세 번째 항도 \(H\) 함수를 사용하여 나타내는 것이 가능하다.
부등식 증명
위의 관계를 이용해서, 우리가 이번 포스팅에서 보이고자 하는 EM 알고리즘의 monotonicity, 식 (*),를 다음과 같이 증명할 수 있다.
\[ \begin{align*} \ell_{\theta^{\left(k\right)}}\left(y\right) & =Q\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{2} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ \tag{3} & \leq Q\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)\\ & =\ell_{\theta^{\left(k+1\right)}}\left(y\right) \end{align*} \]
자 하나씩 살펴보도록 하자. 처음의 등식은 앞에서 살펴본 로그 우도 함수의 Q와 H함수를 사용하여 나타낸 식의 \(\theta\)에 \(\theta^{(k)}\)를 대입한 것이다. 부등식 (2)가 성립하는 이유는 EM 알고리즘의 M-step의 정의에 의하여 성립한다. 왜냐하면 \(\theta^{(k+1)}\)의 정의가 \(Q\) 함수를 최대화시키는 값이기 때문이다. 마지막으로 부등식 (3)의 경우는 다음을 증명해야 한다.
\[ H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\geq H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right) \]
위의 식을 증명에는 H함수의 정의와 통계학과 경제학에서 유명한 Jensen의 부등식이 사용된다.
\[ \begin{align*} & H\left(\theta^{\left(k+1\right)},\theta^{\left(k\right)}\right)-H\left(\theta^{\left(k\right)},\theta^{\left(k\right)}\right)\\ & =\mathbb{E}\left[log\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\\ \tag{4} & \leq log\left(\mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\right)\\ \tag{5} & =log\left(\int\left(\frac{f_{\theta^{\left(k+1\right)}}\left(x|y\right)}{f_{\theta^{\left(k\right)}}\left(x|y\right)}\right)f_{\theta^{\left(k\right)}}\left(x\right)dx\right)\\ \tag{6} & =log\left(\int f_{\theta^{\left(k+1\right)}}\left(x|y\right)dx\right)\\ & = 0 \end{align*} \]
위 부등식 (4)는 log 함수가 concave함수이기 때문에, Jensen의 부등식에 의하여 성립한다. 두 번째의 식 (5)는 기댓값의 정의에 의하여 성립하게 되고, 식 (6)은 확률 밀도 함수의 적분 값이 1이 되어야 하므로 성립하게 된다. 따라서 위의 부등식 (3)이 성립하게 되므로 증명이 끝나게 된다.
위의 정리는 우리가 EM 알고리즘을 반복하면 반복할수록, 얻어진 모수의 값이 반복 횟수를 적게 해서 얻어진 모수 값보다 로그 우도 함수의 값을 증가시키는 모수가 된다는 것이다. 하지만 여기서 중요한 사실은 이 성질이 우리가 발생시킨 모수가 로그우도 함수를 최대로 만드는 글로벌한 optimal값으로 수렴하는 것을 보장해주지는 않는다. 만약 로그우도 함수가 local maxima나 saddle point 같은 정상점들을 많이 가지고 있다면, 그러한 점들로 수렴한 가능성이 있다는 사실에 주의하도록 하자.
마지막 증명에 대한 이해 시각적 이해
앞선 증명 과정에서의 부등식 (4)~(6)이 성립하는 이유는 로그 안의 기댓값이 다음의 부등식을 만족하기 때문이다.
\[ \mathbb{E}\left[\frac{f_{\theta^{\left(k+1\right)}}\left(X|y\right)}{f_{\theta^{\left(k\right)}}\left(X|y\right)}|Y=y,\theta^{\left(k\right)}\right]\leq1\,\,\,\,\,\,a.e.\,w.r.t.\,p_{\theta^{\left(k\right)}} \]
이 부등식을 엄밀하게 설명하기엔 필자의 역량이 아직 부족하다. 하지만 필자가 이해하고 범위 내에서 좀 더 구체적인 예를 들어 설명해보도록 하겠다. 위의 부등식에서 먼저 \(f(x|y)\)는 조건부 확률 밀도 함수이므로 결국 밀도 함수이다. 즉, 두 확률 밀도 함수의 분수 꼴에 입력값인 X가 들어간, likelihood ratio 확률변수의 기댓값이 되는 것이며, 조건의 \(\theta^{(k)}\)는 확률변수 X가 모수 \(\theta^{(k)}\)를 따른다는 것을 의미한다. 이 부분을 좀 더 구체적인 R코드를 들어서 설명하자.
균일 분포 \(U(\theta - 1/2, \theta + 1/2)\)를 따르는 확률변수 \(X_1\)와 \(X_2\)를 생각하자. 그리고 \(\theta^{(1)} = 0.5\), \(\theta^{(2)} = 1\)을 가정하자. 그렇다면 \(X_1\)는 균일분포 \(U(0, 1)\)을 따르고, \(X_2\)는 균일분포 \(U(0.5, 1.5)\)를 따르게 된다. 이 두 확률변수의 pdf는 다음과 같이 그릴 수 있을 것이다. 편의상 \(X_1\) 의 pdf를 \(f\), \(X_2\) 의 pdf를 \(g\)라고 하자.
파란색의 \(X_1\)의 pdf, 빨간색은 \(X_2\)의 pdf가 된다. 그렇다면 이러한 상황에서는 위에서 살펴본 likelihood ratio 함수, \(g(x)/f(x)\), 는 어떠한 모양이 될까?
1에서 1.5 사이는 f의 값이 0, g의 값이 1이 되어, 함숫값이 무한대가 되므로, 그리는 것을 생략하였다. 또한 두 pdf의 값이 0이 되는 부분은 임의로 1로 처리하였다.(이 부분의 처리는 우리의 결괏값과는 무관하다. 왜냐하면 우리가 생각하는 확률변수 \(X\)는 \(\theta^{(1)}\) 따르기 때문이다. 즉, 0에서 1 사이의 값 밖에 나오지 않는다.) 따라서 \(\theta^{(1)}\) 하에서 Likelihood ratio 확률변수의 조건부 기댓값은 다음과 같이 계산할 수 있다.
\[ \begin{align*} & \mathbb{E}\left[\frac{f_{\theta^{\left(2\right)}}\left(X\right)}{f_{\theta^{\left(1\right)}}\left(X\right)}|\theta=\theta^{\left(1\right)}\right]\\ = & \mathbb{E}\left[\frac{g\left(X\right)}{f\left(X\right)}|\theta=0.5\right]\\ = & 0\times\frac{1}{2}+1\times\frac{1}{2}\\ = & \frac{1}{2} \end{align*} \]
위와 같은 경우에 \(\theta^{(1)}\) 하에서 Likelihood의 조건부 기댓값은 분자의 pdf가 분모의 pdf와 같을 때 가장 큰 값, 1, 을 갖게 된다. 위의 경우처럼 정의역이 차이가 나는 경우가 아니더라도 이러한 현상은 똑같이 발생한다. 다음의 R코드를 참고하자.
theta <- seq(-10, 10, by = 0.1)
condEX <-function(theta){
rv_new <-function(x){dnorm(x, mean = theta) / dnorm(x, mean = 0)}
x <- rnorm(10^5, mean = 0)
x <- c(x, -x)
result <- sapply(theta, condEX)
{
emptyPlot(xrange = c(-10, 10), yrange = c(0, 3))
title(main = "Cond. expectation of likelihood ratio under mu = 0",
xlab = "x", ylab = "f(x)/g(x)")
add_points(x = theta, y = result, col = "red", lwd=1.5)
}
위의 그래프에서 \(-5\) 와 \(5\) 근처에서 값이 튀는 이유는 난수를 뽑았는데, 극단치의 값이 많이 나와버려서 표본 평균의 값이 튀어버리는 현상 때문이다. 대략의 트렌드를 보면 1보다 작은 값을 유지하는 것을 알 수 있다. 이 주제와 관련한 좀 더 깊은 이해를 원하는 독자는 ‘contiguity’ 혹은 ’absolutely continuous’의 개념을 구글링 해보기 바란다.
Reference
[1] Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. New York: Springer series in statistics, 2001.
[2] Huang, Jian. The University of Iowa, Advanced Inference I lecture note.
'Statistics' 카테고리의 다른 글
| EM 알고리즘에 대하여 Optimization 강의 1 (0) | 2023.04.05 |
|---|---|
| 메트로폴리스-해스팅스(Metropolis-Hastings) 난수추출 알고리즘에 대하여 (0) | 2022.05.09 |
| [be-favorite] #5 중심극한정리에 관한 고찰 (4) | 2022.01.23 |
| 넷플릭스 DP에 나온 몬티홀 문제와 베이즈 정리에 대한 완벽 정리.zip (0) | 2021.09.27 |
| 세상에서 가장 친절한 MLE 강의 시리즈. 1강 - 개념이해 (0) | 2021.09.25 |




댓글