오늘 나른한 일요일 오후에 R distill 패키지로 블로그를 구축하려고 갔던 별다방에서, 중심극한정리에 대해 다시 생각해보게 되었습니다. 결국, 블로그 구축은 하나도 못하고 말이죠.😂 그래서, 어떤 것들을 고찰했는지 주저리주저리 떠들어 보겠습니다.
중심극한정리에 대한 고찰
수식
다음은 중심극한정리(Central Limit Theorem, CLT)를 표현할 때, 통계학에서 일반적으로 선호하는 아름다운 수식 한 줄입니다:
\begin{align} \sqrt{n} ({\bar{X}}_n - \mu) \ \ \overset{d}{\longrightarrow} \ N(0, \sigma^2) \end{align}
여기서 $\overset{d}{\longrightarrow}$는 분포 수렴(convergence in distribution)을 의미합니다.
분포수렴
분포 수렴은 간략히 설명드리면, 어떤 확률변수열 $X_n$에서 $n$을 무한대로 보내는 경우, $X_n$의 분포가 특정 분포 $X$로 수렴하는 경우, 이를 두고 $X_n$이 특정 분포 $X$로 분포 수렴한다고 정의합니다.
$$X_n \overset{d}{\longrightarrow} X$$
의미
중심극한정리를 이해한다는 목표를 이해하기 위해, 분포수렴은 $n$이 커지면서 일어나는 현상을 나타내는 개념이라는 점을 잘 기억해주시기 바랍니다. 이를 바탕으로 중심 극한 정리를 표현하는 식 (1)이 의미하는 바를 음미해보면, 표본 크기($n$, sample size)를 무한대로 보내면 모집단 분포에 관계없이 표본 평균의 분포는 정규분포를 따른다는 것입니다. 통상적으로 표본 크기 $n$이 30 이상일 때 중심극한정리가 성립한다고 알려져 있습니다. 예를 들어, 미지의 분포를 갖는 모집단으로부터 표본을 표본 크기($n$) 30만큼 추출하여 관측된 값으로 표본평균 $\bar{x}$를 계산 했다고 했을 때, 우리는 별다른 정규성 검정 없이 중심극한정리를 통해 관측된 표본평균은 근사적으로 정규분포를 따른다고 주장할 수 있습니다.
즉, 중심극한정리는 샘플링 횟수(k)와는 무관합니다.
샘플링 횟수에 관한 이야기를 꺼내는 이유는 중심극한정리가 실제로 잘 작동하는 지를 체크해보기 위해 종종 시뮬레이션 스터디를 수행하기 때문입니다. 샘플링 횟수를 많이 가져감으로써 관측된 통계량(e.g. 표본평균)의 값들을 히스토그램으로 쌓기만 하면, 해당 통계량이 갖는 미지의 분포를 경험적으로(empirically) 추정할 수 있기 때문입니다.
예를 들어, 중심극한정리가 실제로 잘 성립한다면 미지의 분포를 갖는 모집단으로부터 표본 크기 n만큼 k번1 샘플링을 한다고 할 때, $n \geq 30$이기만 하면 $k$번 샘플링된 각 표본으로부터 구한 표본평균들이 이루는 분포는 정규분포로 수렴할 것입니다. 반대로 무수히 많은 샘플링 횟수를 가져간다고 하더라도, $n$이 30에 비해 현저히 작으면 표본평균들이 이루는 분포는 정규분포로 수렴된다고 보장할 수 없을겁니다. 본 글에서 직접 R을 이용한 시뮬레이션을 통해 이러한 점들을 알아볼 예정이며, 시뮬레이션 스터디의 결과를 통해 얻은 결론부터 말씀드리면 중심극한정리의 $n \geq 30$이라는 조건은 성립 요건의 일반화를 위해 매우 보수적으로 설정되어 언급되는 값이라는 것입니다.
예를 들어, 모집단 분포로 전 구간에서 표본이 관측될 확률이 동일하고 왜도(skewness)가 0인 symmetric한 형태의 분포를 갖는 연속형 균일분포(continuous uniform distribution)를 중심극한정리가 잘 작동하는 것을 보여주기 위한 시뮬레이션 스터디에 사용하는 경우, 잘못된 오해를 불러일으킬 수 있습니다. 조금 더 깊게 생각해봅시다. 균일분포는 앞서 말씀드렸다시피 전 구간에서 표본이 관측될 확률이 동일한 분포에 해당합니다. 즉, 균일분포를 따르는 모집단으로부터 표본을 추출할 경우 표본의 크기가 30보다 훨씬 작더라도, 추출한 각 표본들에 평균을 취한다면 주어진 구간의 중간 정도의 적당한 값이 표본평균값으로 계산 될 것이고, 이에 따라 관측된 표본평균들을 쌓는다면 그 분포는 표본크기가 작더라도 샘플링 횟수만 키우면 종모양의 정규분포 형태를 띠게 될 가능성이 매우 높을 것입니다. 이를 보고 결코 중심극한정리를 일반화해서는 안됩니다. 백문이 불여일견이니 시뮬레이션 스터디로 보여드리려고 합니다.
시뮬레이션 스터디
먼저, 표본크기($n$)를 1, 10, 30으로 각각 설정하여 0부터 1까지 구간에서 정의되는 연속형 균일분포로 표본을 1000회($k$)씩 추출하여 표본평균들이 이루는 분포를 직접 살펴보았습니다2:

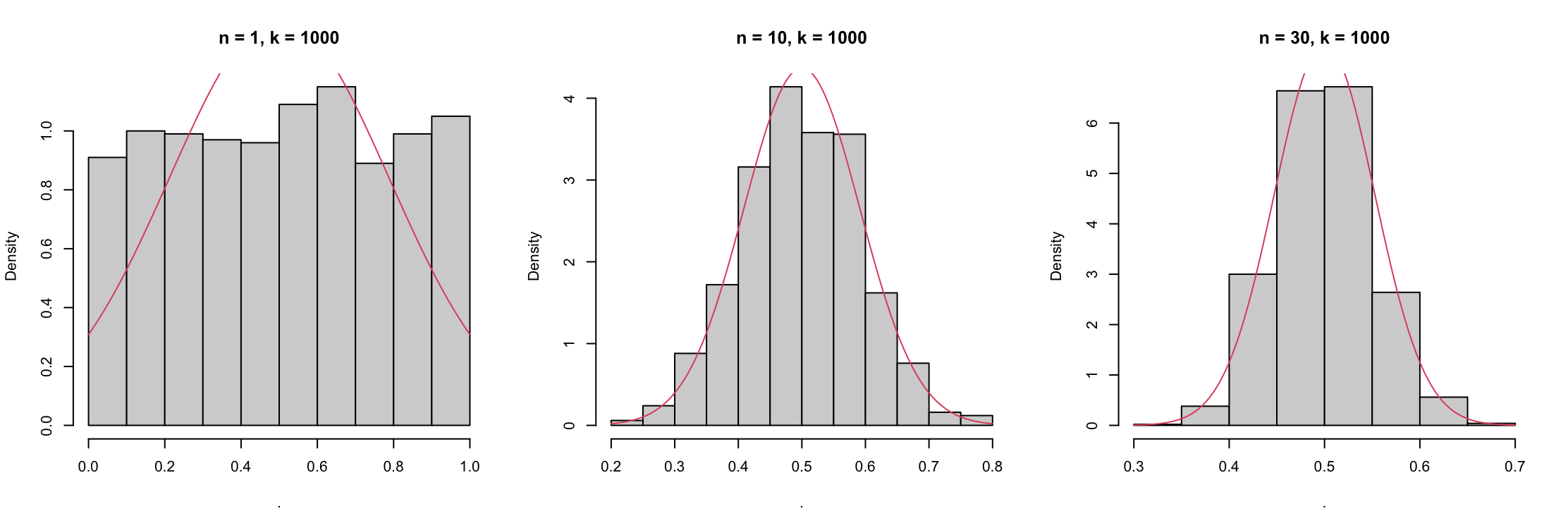
극단적인 예로 표본을 1개씩만 1000번 뽑을 경우 모집단 분포로 수렴하고 있음을 확인할 수 있습니다. 그러나, 표본 크기를 10 정도로만 늘린다고 하더라도 표본 평균들이 이루는 분포는 정규분포에 거의 근사하고 있음을 알 수 있습니다.
자, 그럼 구간마다 표본이 관측될 확률이 다르고 왜도가 큰(치우침이 큰) 모집단 분포로부터 표본들을 추출하는 경우는 어떨까요? 시뮬레이션을 수행하기 전 결론부터 말씀드리면 왜도가 큰(치우침이 큰) 분포 또는 봉우리가 여러 개인 다봉 분포(multimodel distribution)일수록 30개보다 적은 수의 표본크기로는 표본평균들이 이루는 분포는 정규분포로 가정하기 힘들며, 즉 중심 극한 정리가 적용될 수 있는 표본 크기로 통상적으로 언급되는 "30"이라는 숫자는 이러한 상황까지 모두 고려하여 매우 보수적으로 설정된 표본 크기라고 볼 수 있습니다. 이제 이를 확인하기 위해 다시 한번 R을 이용하여 시뮬레이션 스터디를 수행해보겠습니다. 오른쪽으로 꼬리가 긴 분포 형태3를 띠는 형태 모수(shape parameter, $\alpha$)가 2, 척도 모수(scale parameter, $\beta$) 0.5인 감마분포(gamma distribution)로부터 앞선 시뮬레이션과 같은 설정으로 표본을 추출하여 표본 평균들이 이루는 분포를 살펴보았습니다:
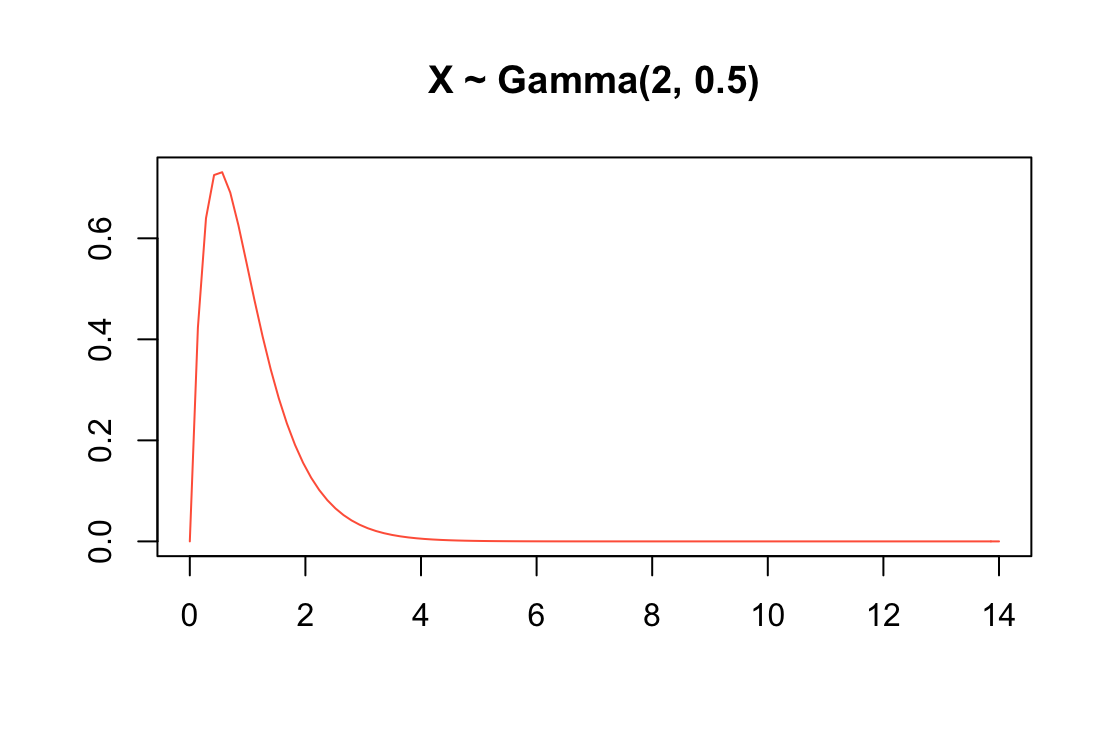

표본 크기가 1인 경우 마찬가지로 모집단 분포의 형태와 거의 동일한 형태를 띠고 있습니다. 그러나, 앞서 살펴본 균일 분포와는 달리 표본 크기가 10인 경우에 표본 평균들이 이루는 분포를 봤을 때는, 이 분포가 정규분포로 근사한다고 보기에는 조금 힘든 부분이 있습니다. 여전히 어느 정도 오른쪽으로 꼬리가 길게 늘어져 있는 형태를 띠고 있죠. 그리고, 그다음으로 표본크기를 30으로 설정한 경우, 이제는 표본평균들이 이루는 분포가 정규분포로 근사하고 있다고 주장할 수 있을만한 형태를 띠고 있는 것을 확인할 수 있습니다.
실제 문제에서 자료를 다룰 때에는, 관측된 통계량이 갖는 미지의 분포에 대해 우리는 알 길이 없습니다. 이에 따라 중심극한정리를 이용하기 위해서는, 표본크기를 30개 이상으로 매우 보수적으로 설정할 수밖에 없다는 점을 기억하시기 바랍니다.
맺음말
저와 같은 통계학 전공자라면 수리통계학(mathematical statistics)이라는 과목을 통해 확률변수, 통계량, 여러 가지 확률분포, 표본분포(sampling distribution), 확률수렴(convergence in probability), 분포수렴 등을 배우며
중심 극한 정리를 배우기 전 수많은 빌드업 단계를 거칩니다.
그래서, 중심극한정리를 어느정도 잘 받아들일 수 있고 앞서 배운 개념들을 잘 이해한 사람이라면 중심극한정리를 “표본평균의 극한분포에 관한 정리”라고 한마디로 간략하게 정리할 수도 있습니다. 그러나, 수리통계학을 딱히 접할 일이 없는 비전공자들의 경우, 중심극한정리를 그저 통계학에서 매우 중요하게 여겨지는 정리라는 이유로 다른 배경지식 없이 접하기 때문에, "표본평균이 분포를 갖는다."는 개념 자체를 받아들이는 것도 어렵고, 이에 따라 중심극한정리를 깊게 음미하기는 매우 힘들다고 생각합니다.
중심극한정리가 통계학에서 아주 중요하게 여겨지는 이유에 대해 간략히 말씀드리면, 통계적 가설검정은 표본평균에 기반한 표본분포(sampling distribution)를 따르는 검정통계량(test statistics)을 통해 진행되기 때문입니다. 이러한 점에서 $n \geq 30$이기만 하면 표본평균에 관한 분포를 정규분포로 가정할 수 있게끔 해주는4 중심극한정리는 통계학에서 상당히 중요하고 자주 언급될 수밖에 없는 정리입니다. 슬통 채널에서 마침 아주 자세히 설명을 해주셨었군요.
통계학은 머릿속에 그림을 그릴 줄 알면 이해가 쉬워진다고 생각합니다. 이러한 점에서 통계학을 접하게 되면 일찍부터 배우는 확률변수(random variable)에 관한 개념을 잘 잡고 가야 한다는 생각이 듭니다. 확률변수를 단지 표본 공간(sample space)에서 정의되는 실숫값을 취하는 함수(real-valued function)라고만 받아들이기보다는, 분포를 갖는다는 점을 머릿속에 인지하고 출발하는 게 중요합니다. 저 또한 전자만을 개념으로 갖고 있을 때는 통계학을 이해하는 폭이 참 좁았던 것 같습니다. 물론, 아직도 이해력과 직관이 너무도 부족하고 이해라기 보단 그저 외우고 있는 것들도 많습니다. 학사, 석사를 모두 통계학 전공으로 마쳤지만, 아직도 너무 어려운 것들이 많네요..😭
이번 포스팅을 통해 중심극한정리에 대해 다시 한번 깊게 고찰했듯이, 여전히 기본적인 개념들이 제 머리를 때릴 때가 종종 있습니다. 수리통계학에 대한 배움은 통계학의 이해에 관한 해상도를 높여주기 때문에, 늘 곁에두고 틈틈히 책을 뒤져가며 공부해야한다고 생각하고 있지만, 사실 수리통계학 책을 펴지 않은지는 참 오래됐습니다. 통계학 전공자로서 다시 한 번 경각심을 가질 필요가 있음 느낍니다.😂
🌱 필자 소개 Taemo Bang (be-favorite)
📝활동 장소
- Github: github.com/be-favorite
- facebook: https://www.facebook.com/profile.php?id=100070120780059
- 개인 블로그: taemobang.com
방태모
안녕하세요, 제 블로그에 오신 것을 환영합니다. 학부, 석사를 통계학으로 전공하고 현재는 지마켓 AI Product 팀에서 Data Science를 하고있습니다. 데이터로부터 인사이트를 추출하는 것을 좋아합니
www.taemobang.com
'Statistics' 카테고리의 다른 글
| EM 알고리즘의 ascent property에 대하여 - Optimization with R (0) | 2023.04.05 |
|---|---|
| 메트로폴리스-해스팅스(Metropolis-Hastings) 난수추출 알고리즘에 대하여 (0) | 2022.05.09 |
| 넷플릭스 DP에 나온 몬티홀 문제와 베이즈 정리에 대한 완벽 정리.zip (0) | 2021.09.27 |
| 세상에서 가장 친절한 MLE 강의 시리즈. 1강 - 개념이해 (0) | 2021.09.25 |
| 확률변수와 모수(parameter)의 관계 (0) | 2020.08.04 |




댓글